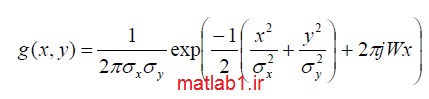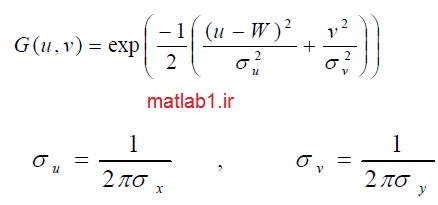يك موجك گابور دوبعدي عبارتست از يك تابع گوسي مدوله شده با يك تابع سيــنوسي مختـلط. اين تـابع را مـي تـوان بـافركانس تابع سينوسيW و انحراف معيارهايσx وσy پـوش تابع گوسي بصورت زير بيان نمود:
توابع گابور يك پاية كامل اما غيرمتعامد را تـشكيل مـي دهنـد.
بسط يك سيگنال بر پاية توابع گابور، توصـيفي از سـيگنال بـافركانس متمركز را فراهم مي سازد. با اينحال اگرچه تابع گابوربا حذف پاسخdc آن مـي توانـد يـك موجـك قابـــل قبـول قلمداد شود ، ليكن اين تابع به يك پاية متعامـد منجـر نخواهـدشد. از اينـرو تبـديل موجـك برپايـة موجـك گـابور، حـاويافزونگ ي است.
در اين بررسي منظـور از موجـك گـابور، بـانكي از فيلترهـايگابور نرماليزه شده است كه بگونـه اي طراحـي شـده انـد كـهنمايش آنها، درجة افزونگي پاييني را شامل شود.
هرگاهg(x,y) را بتو ان يك موجك گابور مادر درنظـر گرفـت، آنگاه خانواده موجكهـاي گـابور از طريـق انبـساط و چـرخش موجك گابور g(x,y) بدست مي آيند:
براي هر تصوير مورد نظر، تبديل موجك گابور آن عبارتست از :
فرض مي كنيم نواحي بافت موضعي ، از نظر مكاني همگن ميباشند ميانگين μmn و انحراف معيار σmn ضرايب تبديل مشخص نمودن نواحي جهت كلاسه بندي بكار مي روند.
حال با استفاده از مقادير ويژگي σmn و μmn يك بردار ويژگي تشكيل مي دهيم.
با فرض آنكه شاخصهاي j و i نمايانگر تصاوير آزمون و مرجع باشند ، فاصله بين تصاوير آزمون و مرجع در فضاي ويژگي بصورت زير تعريف مي شود :