رندوم فارست

(بر روی تصویر بالا کلیک کنید)

در سال 2001، Breiman الگوریتم رندوم فارست را ارائه داد که یک حالت عمومی‌تر از بگینگ به حساب می‌آید و در واقع یک لایه رندوم به بگینگ اضافه می‌کند. در این الگوریتم علاوه بر اینکه هر درخت با استفاده از سمپل‌های متفاوتی از داده‌ها ساخته می‌شود، روند ساخت درخت‌ها نیز تغییر می‌کند. در واقع در یک درخت استاندارد، هر گره تصمیم با استفاده از بهترین نقطه شکست انتخاب از میان همه خصیصه‌ها شکسته می‌شود، اما در رندوم فارست، هر گره تصمیم بر مبنای بهترین نقطه شکست از میان زیرمجموعه‌ای از خصیصه‌هایی که بطور رندوم در سطح آن گره انتخاب شده اند، شکسته می‌شود [30]. معماری کلی مربوط به رندوم فارست برگرفته از [31] در شکل1-2 آمده است.

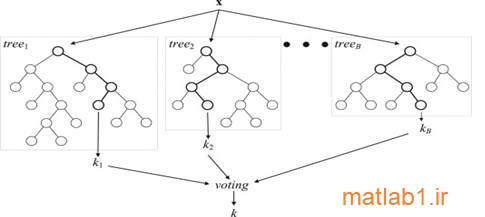
شکل 2-2. نمایی کلی از الگوریتم رندوم فارست که یک متد یادگیری تجمعی برای کلاسه‌بندی و رگرسیون است. مدل‌های پایه، درختان تصمیم‌گیری CART هستند و خروجی نهایی K، بر اساس رای‌گیری خروجی‌های B عدد درخت تعیین می‌شود. در مورد کلاسه‌بندی، رای نهایی بر مبنای مُد خروجی‌ها و در مورد رگرسیون بر اساس میانگین‌گیری تعیین می‌شود.

بکارگیری این استراتژی باعث عملکرد مناسب و کارا در مقایسه با دیگر الگوریتم‌ها همچون آنالیزهای جداسازی، بردارهای پشتیبان کننده و شبکه‌های عصبی مصنوعی می‌شود. همچنین این تکنیک فقط به تنظیم دو پارامتر (1) تعداد متغیرهای قرار گرفته در زیرمجموعه‌ی رندوم انتخاب شده و (2) تعداد درختان مورد استفاده، نیاز دارد و علاوه بر آن، حساسیت شدیدی نسبت به مقادیر این پارامترها ندارد.

2-3-1. مراحل توسعه‌ی رندوم فارست
بطور کلی الگوریتم رندوم فارست یک مجموعه از درخت‌های شبه CART است . مروری کلی بر این الگوریتم را تحت 4 مبحث 1) مرحله رشد درختان ، 2) مرحله ترکیب درختان ، 3) مرحله خودآزمایی و 4) مرحله پس پردازش بررسی می‌کنیم که این مباحث از [32] آمده است.
1) مرحله رشد درختان:
درختان موجود در رندوم فارست، شاخه‌های دوتایی دارند، یعنی هر والد، تنها به دو فرزند تقسیم می‌شود. رندوم بودن در دو مرحله به هرکدام از این درختان تزریق می‌شود، (1) در توسعه هر درخت روی نمونه‌های رندوم انتخاب شده از داده آموزشی و (2) در مرحله انتخاب بهترین نقطه شکست از میان متغیرهایی که بطور رندوم از میان همه متغیرها انتخاب شده‌اند. اگر m، تعداد کل خصیصه‌ها باشد، مقادیری که Breiman برای تعداد متغیرهای انتخابی R پیشنهاد داد، به ترتیب در فرمول‌های (2-1)، (2-2) و (2-3) بدین ترتیب بود:

انتخاب زیرمجموعه‌ای از خصیصه‌ها و توسعه‌ی درختان براساس آن‌ها منجر به افزایش سرعت رشد درختان و همچنین عدم نیاز به اعمال الگوریتم‌های انتخاب خصیصه می‌شود.
2) انتخاب نقطه شکست در رندوم فارست:
هرچند انتخاب بهترین نقطه شکست از زیرمجموعه رندوم، ممکن است لزوماً بهترین نتیجه را در بر نداشته باشد، اما تکرار این انتخاب‌ها در مورد هرگره، تصمیم‌گیری متفاوتی را در طی ساخت درخت فراهم می‌کند و نهایتاً متغیرهای مهم نیز در ساخت درخت دخیل خواهند شد. این موضوع دلیلی است در راستای تأکید بر استفاده از درخت‌های با سایز کامل، که هَرَس نشده باشند. نتایج تحقیقات نیز نشان داده‌اند که هَرس کردن این درختان منجر به کاهش کارآیی الگوریتم می‌شود.
3) مرحله خودآزمایی در رندوم فارست:
در طی اعمال الگوریتم رندوم فارست با توجه به مرحله نمونه برداری bootstrap، هر درخت تقریبا بر روی 63% از داده‌ها، رشد پیدا می‌کند. بنابراین 37% از داده‌ها، در مورد هر درخت استفاده نمی‌شود که به این داده‌ها “Out Of Bag” یا به اختصار OOB می‌گویند. از داده‌های OOB که در مورد هر درخت داده‌های مجزایی هستند ، می‌توان برای ارزیابی درختان توسعه یافته استفاده کرد. در واقع با استفاده از این مجموعه داده‌های OOB، الگوریتم رندوم فارست می‌تواند آمارهایی مربوط به کارآیی الگوریتم خود ارائه دهد. همچنین مسئله RF Self-testing، شبیه مسئله وارسی اعتبار می‌باشد که هر بار روی قسمت بندی‌های متفاوتی از داده اولیه محاسبه می‌شوند. بنابراین با استفاده از این قابلیت رندوم فارست، حتی اگر کل داده آموزشی بعنوان ورودی الگوریتم استفاده شود، امکان Self-testing در طی یادگیری فراهم است. علاوه برآن، این قابلیت در مورد داده‌های کوچک حائز اهمیت زیادی است، چرا که نیازی به کنار گذاشتن قسمتی از داده برای تست، لازم نیست. بنابراین از جمله الگوریتم‌های پرکاربرد در خصوص اعمال بر روی داده‌های کم سایز محسوب می‌شود. از دیگر نتایج وجود داده‌هایOOB در هنگام ساخت درخت، مقاومت در برابر مسئله بیش برازش و عمومیت‌بخشی در برابر داده‌های جدید، می‌باشد. همچنین با انتخاب زیرمجموعه¬ای از خصیصه‌ها، نیازی به اعمال الگوریتم‌های انتخاب ویژگی نیز نخواهد بود[21].
4) مرحله پس پردازش در رندوم فارست:
در واقع پس از ساخت درختان، با دقت در آنها، دید بهتری در مورد داده می‌توان بدست آورد. با در نظر گرفتن هر رکورد، می‌توان تعداد دفعاتی که هر دو رکورد در برگ‌های یکسان درختان قرار گرفته‌اند، را محاسبه کرد و میزان شباهت آن‌ها را بدست آورد. معیار فاصله بدست آمده از این طریق می‌تواند برای ساخت ماتریس عدم شباهت نیز استفاده شود که بعنوان ورودی الگوریتم‌های خوشه یابی سلسله مراتبی بسیار پرکاربردند. همچنین با حرکت روی مسیر درختان، عملاً مکانیزم الگوریتم نزدیکترین همسایگی انجام می‌شود. در نظر بگیرید که برای رسیدن به یک گره در درخت، یک رکورد باید تمام شرایط در همه والدها را ارضا کند، بنابراین رسیدن دو رکورد به یک گره نشان دهنده شباهت آن‌هاست. پس همانند تکنیک نزدیکترین همسایگی که با توجه به شبیه‌ترین همسایه‌ها، بر چسب آن داده جدید را پیش¬بینی می‌کند، درختان موجود در رندوم فارست نیز همانند این روند را می‌توانند دنبال کنند.
5) مرحله ترکیب درختان در رندوم فارست:
از آنجا که در متدهای یادگیری تجمعی نهایتاً یک مدل نهایی ارائه می‌شود، پس در اینجا نیز درخت‌های آموزش دیده، باید ترکیب شوند. همانطور که پیشتر بیان شد، در مورد مسائل کلاسه بندی، بین نتایج مدل‌ها رأی‌گیری و در مورد مسائل رگرسیون از نتایج مدل‌ها میانگین‌گیری می‌شود. همچنین ترکیب مدل‌ها می‌تواند بر اساس نوعی وزن‌دهی صورت گیرد، یعنی همه مدل‌ها به یک اندازه در مدل نهایی مشارکت نداشته باشند. از جمله تلاش‌هایی که در این زمینه صورت گرفته می‌توان به موارد [33] و [34] اشاره کرد. در اکثریت این تحقیقات، وزن‌دهی و میزان مشارکت یک مدل، بر اساس دقت آن تعیین می‌شود.

2-3-2. تئوری‌های مرتبط با رندوم فارست
در این بخش به بیان تعاریف ریاضی موجود از رندوم فارست می‌پردازیم که در مقاله اصلی [21] در مورد رندوم فارست آمده است. همچنین تئوری‌های مرتبط با این الگوریتم همچون مسئله همگرایی، دقت و خطای عمومی آن را بررسی می‌کنیم. علاوه بر آن به معرفی مجموعه OOB پرداخته و چگونگی کاربرد آن را برای محاسبه قدرت، وابستگی و مشاهده خطا در روند ساخت الگوریتم توضیح می‌دهیم. همچنین، از آنجا که تمرکز اصلی این پایان نامه با توجه به داده‌های ترافیکی، انجام رگرسیون است، بنابراین مسئله رگرسیون رندوم فارست را نیز بررسی کرده و در انتها، مزایا و کاربردهای الگوریتم رندوم فارست را توضیح می‌دهیم.
تعریف ریاضی رندوم فارست: “یک رندوم فارست یک کلاسه بند است که از مجموعه ای (k عدد) از کلاسه بندی‌های با ساختار درختی تشکیل شده که بردارهای رندوم مستقل و یکنواخت توزیع شده هستند و هرکدام از درخت‌ها یک رأی واحد را برای مشهورترین کلاس با ورودی x تعیین می‌کنند” [21].
“بعبارتی برای kاُمین درخت یک بردار رندوم تولید شده که مستقل از بردارهای رندوم قبلی یعنی است، اما توزیع یکسانی دارد و هر درخت با استفاده از مجموعه آموزشی و رشد پیدا می‌کند. نهایتاً هر درخت، یک کلاسه بند را نتیجه خواهد داد که X یک بردار ورودی است”[21]. الگوریتم رندوم فارست بصورت شبه کُد در شکل 2-3 (برگرفته از [32]) آورده شده است.

Algorithm Random Forest (k)
Input : Sequence of N examples  <( x1 ,y1 ),….., ( xN, yN )>  with labels   y i€ Y={ 1,…,L }
Distribution D over the N example
Integer K specifying number of iterations
p = # of variables
Do For t=1,2,.., K(# trees)
• Choose bootstrap sample Di from D to construct tree Ti
• Select m input variables at random from p
       o (m<<p)
       o To determine the decision tree at a node of the tree
• Calculate the best split based on these m variables in the training set
End

Choose the class that receives the highest total vote as the final classification.

شکل 2-3. معماری کلی مربوط به الگوریتم رندوم فارست. در طی رشدK عدد درخت، توسعه‌ی هر درخت روی نمونه‌های رندوم انتخاب شده Di صورت گرفته و از میان p خصیصه‌ی نمونه‌ها، m خصیصه بطور رندوم انتخاب می‌شوند.
در قسمت بعدی نیز، در راستای توصیف دقت رندوم فارست ، نگاهی کلی به مسائل همگرایی رندوم فارست و خطای عمومی این الگوریتم که توسط Breiman بیان شده‌اند، خواهیم داشت[21].