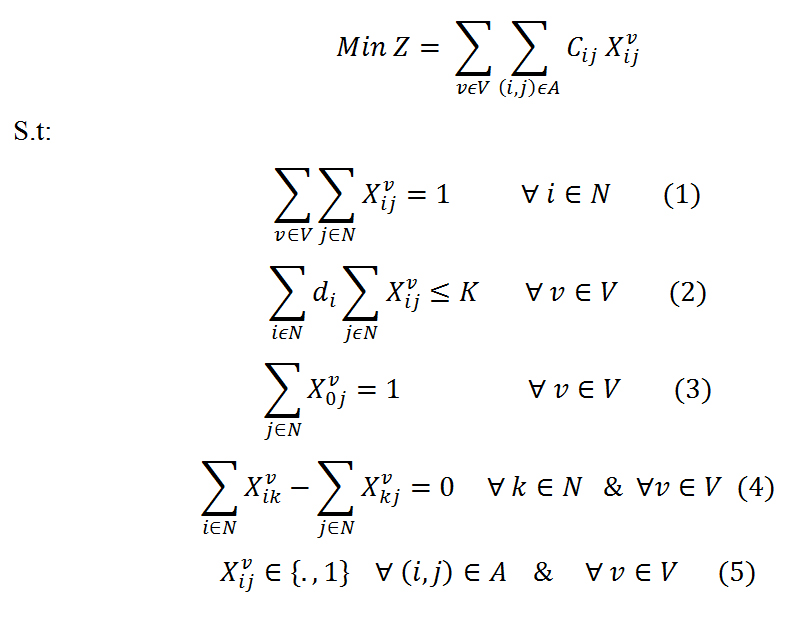چکیده
چکیده
طراحی شبکه های توزیع و جمعآوری یکی از مهمترین مسائل مطرح در صنایع کنونی جهان است. در این صنایع، مسیر یابی وسایل حمل و نقل در نظر گرفته شده و مدل [۱]VRP را شکل دادهاند، به این معنا که مسیر بهینهی هر وسیلهی نقلیه در مسیر مرتبط خود تعیین شود. یکی از کاربردهای این مساله در سیستم جمعآوری زبالههای شهری است. اما مسالهی اصلی در این سیستمها اینست که علاوه تعیین مکانهای استقرار وسایل نقلیه (وسایل حمل زباله)، بایستی مکانهای مراکز میانی تخلیه زبالهها نیز تعیین شود و در عین حال وسایل نقلیه به صورت بهینه مسیریابی شوند. در این مقاله روشی یکپارچه برای حل این مساله با استفده از الگوریتم ژنتیک آمده است.
کلمات کلیدی: مسیریابی وسایل نقلیه، سیستم جمعآوری زباله، الگوریتم ژنتیک
۱- مقدمه
مساله مسیریابی وسیله نقلیه یکی از مهمترین مسائل موجود در صنایع جهان است که امروزه به علت کاربردهای واقعی در مسائل صنعتی بسیار مورد توجه قرار گرفته است. در این مساله چندین وسیله نقلیه بطور همزمان از انبار (پارکینگ وسایل نقلیه) شروع به حرکت کرده و بعد از ملاقات کردن گرههای تقاضا (مشتریان) به انبار باز میگردند، به شرط آنکه اولاً هر گرهی تقاضا فقط توسط یکی از این وسایل نقلیه ملاقات شود و ثانیاً هر وسیله نقلیه بیشتر از ظرفیت خود در طول مسیر بارگذاری نکند. به کاربردن صحيح اين مساله حدود ۵ تا ۲۰ درصد در کل هزينهي حمل و نقل صرفهجويي ميکند.
از کاربردهای اصلی این مساله میتوان به جمع آوری زباله، توزیع و پخش مواد غذایی و دارو، مسیریابی سرویس مدارس و کارمندان، توزیع و پخش نامههای پستی، برنامهریزی مسیر کشتیها، توزیع روزنامه، حرکت رباتها در کف کارخانه اشاره کرد.
اهدافی مختلفی تا به حال برای این مساله در نظر گرفته شده است که تعدادی از آنها عبارتند از:
· کمینه کردن مسیر پیموده شده توسط همه وسائل نقلیه
· کمینه کردن کل تعداد وسایل نقلیه
· کمینه کردن تابعی از زمان های دیرکرد یا زودکرد خدمت رسانی وسایل نقلیه به مشتریان
VRP میتواند دارای محدودیتهای متفاوتی باشد. برخی از این محدودیتها عبارتند از: تعداد مراکز سرویس دهی، محدود بودن یا نامحدود بودن ظرفیت خودروها، قطعی یا احتمالی بودن تقاضا، وجود یا عدم وجود محدودیت برای طول مسیر.
مساله VRPاز مسائل مشهور عدد صحيح است که در دسته مسائل NP-Hard قرار ميگيرد. پيچيدگي اين مساله مربوط به دو مساله زير است:
۱-مساله فروشنده دوره گرد(Travel Salesman Problem)
اگر ظرفيت وسيله ي نقليه نامحدود در نظر گرفته شود VRP تبديل به مساله چند فروشنده دوره گرد([۲]MTSP) مي شود.
۲-مساله پوشش(Bin Packing Problem)
اين سوال که آيا يک جواب براي مساله VRP امکان پذير است يک مساله پوشش است.
انواع مسائل VRP
مساله VRP انواع مختلفي دارد که هر کدام شرايط مختلفي را در نظر ميگيرند. هر يک از اينها داراي تابع هدف، فضاي امکان پذير و مدل رياضي خاص خود است. تعدادی از اين مسائل عبارتند از: CVRP،MDVRP، PVRP، SDVRP، SVRP، VRPTW و VRPPD
به عنوان مثال [۳]CVRPTWهمان مساله VRP است با اين تفاوت که هر وسيله نقليه ظرفيت يکنواختي از يک جنس خاص دارد. در مساله جمعآوری زباله نیز ما به دلیل محدودیت در ظرفیت وسایل نقلیه با این مساله روبرو هستیم.
۲- ادبیات موضوع
با توجه به اهداف و محدودیتهای تعریف شده برای VRP و در نظر گرفتن عواملی مانند زمان و هزینههای مورد نیاز جهت رسیدن به جواب و دقت مطلوب، روشهای مختلفی برای بدست آوردن جواب VRP وجود دارد که بطور کلی به سه دسته روشهای دقیق، ابتکاری و فراابتکاری تقسیمبندی میشوند.
روشهای دقیق:
در دهههای ۱۹۶۰ و ۱۹۷۰ میلادی عمده تحقیقات انجام گرفته برای حل VRP بر روی روشهای دقیق متمرکز بود که برخی از آنها عبارتند از: برنامهریزی پویا، روش تبدیل VRP به TSP و فرمولبندی دو اندیسی.
تبدیل VRP به :TSP
در این روش شبکه مورد نظر با اضافه کردن چند گره و یال مجازی تبدیل به شبکه دیگری می شود، که شبکه بدست آمده به صورت یک مساله TSP خواهد بود و با حل TSP میتوان مسیرهای مورد نظر و تعداد وسایل مورد نیاز را تعیین نمود.[۱[
برنامه ریزی پویا:
نمونهای از کاربرد برنامه ریزی پویا در حل VRP توسط ایلیون برای m خودرو که ظرفیت آنها مشخص میباشد، ارائه شده است. در این تحقیق با تبدیل VRP به m مساله TSP جواب بهینه محاسبه گردیده است. [۱]
فرمول بندی سه اندیسی :
این فرمول بندی توسط فیشر ۳ و جی کومار ۴ ارائه گردیده است. فرمول بندی ارائه شده مساله تخصیص عمومی و مساله فروشنده دوره گرد با محدودیت زمانی را پوشش میدهد. این روش ابتدا یک مساله اصلی GAP را برای تخصیص دادن نقاط به خودروها حل کرده و سپس بهترین مسیر برای هر خودرو از طریق حل یک TSPTW بدست میآید. [ ۲ و ۳ و ۱[
روشهای ابتکاری:
VRP و TSP جزء مسائل Np- hard یا Np- complete میباشند[ ۴ ] و با افزایش اندازه مساله حجم محاسباتی روشهای شناخته شده برای حل بهینه آنها دارای رشد نمایی است، بنابراین حل بهینه مسائل واقعی با اندازه بزرگ تقریبا غیر عملی است و به ناچار باید از روشهای ابتکاری و فراابتکاری برای محاسبه جواب قابل قبول و تقریباً بهینه استفاده شود. برخی از الگوریتم های ابتکاری VRP در ادامه آمده است.
الگوریتم صرفه جویی ( C& W)
این الگوریتم اولین بار توسط کلارک و رایت برای حل مسائل VRP با محدودیت ظرفیت و با تعداد نقاط محدود ارائه شد. این روش با ایجاد مسیرهایی که شامل مرکز و یک نقطه تقاضای دیگر است، شروع شده و در هر مرحله با توجه به بیشترین صرفه جویی ممکن دو مسیر با هم ترکیب میشود.[۱,۲]
تعداد مسیرها( خودروها) توسط الگوریتم مشخص میشود ولی در صورتیکه تعداد خودروها از قبل مشخص باشد، میتوان ترکیب مسیرها را تا جایی ادامه داد که تعداد مسیرهای موجود با تعداد مشخص شده برابر شود، حتی اگر میزان صرفه جویی منفی باشد.
الگوریتم جارو :
این الگوریتم توسط ژیلت و میلر ارائه گردیده و بر اساس روشهای دسته بندی مسیریابی عمل میکند. در این روش به مراکز تقاضا مختصات قطبی تخصیص داده میشود و بر اساس افزایش زاویه رتبه بندی میشوند. از مرکزی که دارای کوچکترین زاویه بوده و به هیچ مسیری تعلق ندارد شروع و تا جایی که ظرفیت خودرو اجازه دهد، مراکز به خودرو اختصاص یافته و مسیر بهینه هر خودرو از طریق حل TSP بدست میآید. در بین مسیرهای مجاور در صورتی که تغییر بعضی از نقاط بین دو مسیر، مسافت کل را کاهش دهد، تغییرات انجام و مجدداً مسیر بهینه هر خودرو محاسبه میشود. کوچکترین مقدار بین جوابهای بدست آمده جواب VRP است.[۱,۲]
الگوریتم مسیر یابی کمانی:
این الگوریتم جزء طبقه مسیریابی دسته بندی بوده و توسط استرن و درور در مورد مسیر یابی متصدیان خواندن کنتور برق ارائه شده است. الگوریتم طی دو فاز مسیرهای بهینه را محاسبه میکند. در فاز اول با استفاده از روشهای CPP یک مسیر اولر ایجاد میشود و در فاز دوم با توجه به محدودیتها مراکز تقاضا دسته بندی میشوند.[۵]
الگوریتم صرفه جویی برای مسیر یابی کمانی:
الگوریتم فوق مشابه الگوریتم صرفه جویی در مسیریابی گرهای بوده و توسط گلدن و وانگ ارائه گردیده است. در این الگوریتم همه مراکز تقاضا در مسیرهای جداگانه قرار گرفته و با توجه به محدودیتهای موجود ترکیب زوج مسیر های ممکن بررسی و دو مسیری که بیشترین صرفه جویی را ایجاد میکند، با یکدیگر ترکیب میشوند.[۶]
روشهای فراابتکاری:
الگوریتمهای فراابتکاری بسیاری درحل مساله مسیریابی خودروها استفاده شده که از آن جمله میتوان به الگوریتم ژنتیک اشاره نمود. استفاده از این الگوریتم در حلVRP، توسط افراد مختلفی بررسی گردیده که به عنوان نمونه می توان به تحقیقات پریرا، تاوارس ، ماچادا و کاستا اشاره نمود. در این تحقیقات کاربرد الگوریتم ژنتیک در مسائل مسیریابی با محدودیت ظرفیت ( CVRP) و مسیریابی با محدودیت زمانی ( VRPTW) بررسی گردیده است. نتایج محاسباتی نشان دهنده کارائی بالای این روش است [۷,۸,۹]. نمونهای از تلاشهای انجام شده برای استفاده از الگوریتم جستجوی ممنوع و سیستم بهینه سازی مورچگان در مراجع ۱۰ و ۱۱ موجود است.
۳- مدل ریاضی
در این قسمت به بیان مدل ریاضی مساله CVRP پرداخته میشود.
محدودیت ۲ تضمین میکند که هر مشتری فقط توسط یک وسیله سرویس بگیرد. در محدودیت ۳ قید ظرفیت ماشینها اعمال میگردد. به عبارت دیگر مجموع حجم تقاضای مشتریانی که به یک ماشین تخصیص داده میشود بایستی حداکثر برابر با ظرفیت ماشین باشد. معادلات ۴ و ۵ تضمین میکند که مسیرها پیوسته باشند. در این معادلات موازنه جریان ورود و خروج وسایل نشان داده شده است. به عبارت دیگر تعداد ماشینهایی که به هر گره وارد میشود برابر با تعداد ماشینهایی است که از آنها خارج میشوند.
متدولوژی حل
برای حل این مساله در حالت جمعآوری زباله از الگوریتم ژنتیک استفاده شده است. الگوريتمهاي ژنتيک از اصول انتخاب طبيعي داروين براي يافتن فرمول بهينه جهت پيش بيني يا تطبيق الگو استفاده ميکنند. قانون انتخاب طبيعي بدين صورت است كه تنها گونههايي از يك جمعيت ادامه نسل ميدهند كه بهترين خصوصيات را داشته باشند و آنهايي كه اين خصوصيات را نداشته باشند به تدريج و در طي زمان از بين ميروند. موتور الگوريتم ژنتيک يک جمعيت اوليه تصادفي از پاسخ هاي ممكن براي مسئله ايجاد ميکند كه هريك از اين پاسخها در قالب يك كروموزوم داراي تعدادي ژن ( هر ژن نماينده ي يك مجهول مسئله مي باشد) بوده و به صورت مناسبي كدگذاري شدهاند. در مرحله بعدي هر كروموزوم در برابر مجموعهاي از معيارها مورد آزمايش قرار ميگيرد. تابع برازش با توجه به ميزان موفقيت هر كروموزوم در حل مسئله ارزش آنها را معين ميكند. سپس بر اساس اين ارزشها كروموزومها به ترتيب صعودي به نزولي مرتب مي شوند تا x% از آنها حفظ شده و بقيه حذف شوند. براي جايگزيني اين كروموزومهاي حذف شده، كروموزومهاي باقيمانده به نحوي دو به دو انتخاب شده و توليد فرزند ميكنند. يك نحوهي اين انتخاب اينست كه مجموعه كوچكي از كروموزومها به صورت تصادفي انتخاب شده و سپس از بين اين كروموزومها، دو كروموزومي كه داراي ارزش بيشتري هستند بهعنوان والدين براي توليد فرزند انتخاب ميشوند. شرايط خاتمه الگوريتمهاي ژنتيک عبارتند از:
· بودجه اختصاص داده شده تمام شود(زمان محاسبه/پول).
· يک فرد(فرزند توليد شده) پيدا شود که مينيمم (کمترين)ملاک را برآورده کند.
· بيشترين درجه برازش فرزندان حاصل شود يا ديگر نتايج بهتري حاصل نشود.
· بازرسي دستي.
· ترکيبهاي بالا.
روشهاي نمايش
قبل از اين که يک الگوريتم ژنتيک براي يک مسئله اجرا شود، يک روش براي کد کردن ژنومها به زبان کامپيوتر بايد به کار رود. يکي از روشهاي معمول کد کردن به صورت رشته هاي باينري است(رشته هاي ۰و۱). يک راه حل مشابه ديگر کدکردن راه حلها در آرايهاي از اعداد صحيح يا اعشاري است،که دوباره هر جايگاه يک جنبه از ويژگيها را نشان ميدهد. الگوريتمهاي ژنتيکي که براي آموزش شبکههاي عصبي استفاده ميشوند، از اين روش بهره ميگيرند. سومين روش براي نمايش صفات در يک GA يک رشته از حروف است که هر حرف دوباره نمايش دهنده يک خصوصيت از راه حل است. در این مساله ما از کدگذاری عدد صحیح استفاده کردیم، به اینصورت که هر کروموزوم توالی گرههای تقاضا در مسیرها را نشان میدهد.
روش هاي انتخاب
روش هاي مختلفي براي الگوريتمهاي ژنتيک وجود دارند که ميتوان براي انتخاب كروموزومهاي والد از آنها استفاده کرد. تعدادی از این روشها عبارتند از:
۱. انتخاب Elitist : مناسبترين عضو هر اجتماع انتخاب ميشود.
۲. انتخاب Roulette : يک روش انتخاب است که در آن عنصري که عدد برازش(تناسب) بيشتري داشته باشد، انتخاب ميشود.
۳. انتخاب Scaling : به موازات افزايش متوسط عدد برازش جامعه،سنگيني انتخاب هم بيشتر مي شود وجزئيتر. اين روش وقتي کاربرد دارد که مجموعه داراي عناصري باشد که عدد برازش بزرگي دارند وفقط تفاوتهاي کوچکي آنها را از هم تفکيک ميکند.
۴. انتخاب Tournament : يک زير مجموعه از كروموزومهاي يک جامعه انتخاب ميشوند و اعضاي آن مجموعه با هم رقابت ميکنند و سرانجام فقط دو كروموزوم از هر زير گروه براي توليد انتخاب ميشوند.
بعضي از روشهاي ديگر عبارتند از:Rank Selection, Generational Selection, Steady-State Selection .Hierarchical Selection
عملگر تقاطع:
در این عملگر که Crossover نام دارد، ۲ کروموزوم براي معاوضه ژنهایشان انتخاب ميشوند. اين فرآيند بر اساس فرآيند ترکيب کروموزومها در طول توليد مثل در موجودات زنده شبيه سازي شده است. اغلب روشهاي معمول Crossover از نوع Single-point Crossover هستند، که نقطه تعويض در جايي تصادفي بين ژنهاي كروموزومها است. بخش اول قبل از نقطه و بخش دوم سگمنت بعد از آن ادامه پيدا ميکند،که هر قسمت برگرفته از يک والد است.
عملگر جهش:
این عملگر دقیقاً مثل جهش در موجودات زنده است که عبارت است از تغيير يک ژن به ديگري. در الگوريتم ژنتيک جهش تغيير کوچکي در يک ژن از کد كروموزوم ايجاد ميکند.