ارزیابی دقت الگوریتمهای چندکلاسه، به علت تعداد زیاد مجموعه دادههای مورد آزمایش و تعداد متنوع روشهای اعمال شده و همچنین خصوصیات مجموعه دادهها که هم شامل دادههای متوازن و هم دادههای نامتوازن میشود ، نیاز به اتخاذ روشهای پیچیدهای دارد.
در حوزه مسائل چندکلاسه، به طور مرسوم، تنها دقت بدست آمده از دستهبندی به عنوان معیار پایه ارزیابی و عمومیت، گزارش میشود [52,53] که به صورت زیر تعریف میشود:
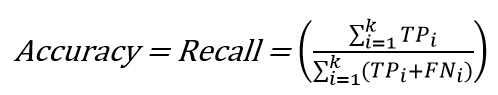
که در این رابطه، نشان دهنده برچسب کلاس است و تعداد کل کلاسهای موجود در مجموعه داده است. گاهی به جای گزارش کردن دقت، نرخ خطای کل[1] نیز گزارش میشود، که همان میباشد. با این حال، صرف گزارش کردن دقت نمیتواند معیار خوبی برای مقایسه باشد؛ چرا که، بهعنوان مثال، این معیار در مواجهه با دادههای نامتوازن بسیار گمراهکننده است [54,55,33]. دلیل این امر آن است که امکان دارد کلاس اقلیت در مقایسه با کلاس اکثریت قابل اغماض باشد، بنابراین در این شرایط حتی اگر تمام نمونههای مربوط به کلاس اقلیت، اشتباه دستهبندی شوند تاثیر زیادی بر دقت نهایی نخواهد داشت.
معیار قابل اعتمادتر برای مقایسه دقت، در مواجهه با دادههای دارای توزیع جهتدار[2]، میانگین هندسی[3] است. سان و همکاران [56] نشان دادند که چگونه میتوان این معیار را برای موارد چندکلاسه به صورت زیر استعمال کرد:
[1] Total error rate
[2] Biased
[3] Geometric mean (G-mean)
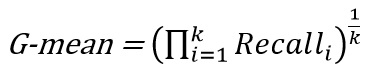
که یک مقدار را تولید میکند که نمایانگر کارایی متوازن دستهبندیکننده در قبال همه کلاسها است. برای آنالیز جامعتر یک دستهبندیکننده در سطح هر کلاس، میتوان از معیار استفاده کرد. این معیار، صراحت هر کلاس که به صورت زیر بهدست میآید را مورد استفاده قرار میدهد:
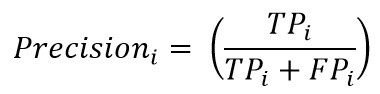
برای هر کلاس به صورت زیر محاسبه میشود:

معیار مقداری بین 0 و 1 تولید میکند که هر چه مقدار و بیشتر باشد، اندازه این معیار هم بزرگتر خواهد بود.