استراتژ يهاي تکاملي خانواده اي از الگوريتمهاي پردازش تکاملي هستند که معمولا براي بهينه سازيهاي عددي مورد استفاده قرار مي گيرند. اين الگوريتمها اول بار توسط رشنبرگ و شفل در دهه 1970 در دانشهگاه برليهن آلمان معرفي گرديدند. اين خانواده از الگوريتمهاي تکاملي در قياس با ساير الگوريتمهاي تکاملي از سرعت به نسبت بالاتري برخوردار بوده و براي مسايل بهينه سازي مرتبط با اعداد حقيقي ميتوانند پاسخ هاي مناسبي را دربر داشته باشند. همانند ساير الگوريتمهاي تکاملي در اين الگوريتمها نيز هدف پيدا کردن مينيمم يا ماکزيمم مناسب بوده و تضميني براي يافتن بهترين جواب در مسايل چند قله اي و پيچيده وجود ندارد. از ويژگي هاي ديگر اين الگوريتمها مي توان به پايه نظري قوي آنها اشاره نمود که در اين خصوص در مقابل عمده ساير رو شهاي تکاملي داراي اثبات رياضي مي باشند.
در اين خانواده از الگوريتمها ، عملگر اصلي ايجاد تنوع، عملگر جهش مي باشد که با اضافه نمودن نويز کنترل شده به مجموعه والد فرزندان آنها توليد مي گردد. اين نويز معمولاً متغيري تصادفي با توزيع نرمال است که به هر يک از مولفه هاي جمعيت اضافه مي شود. از طريق تنظيم واريانس اين نويز به صورت همزمان با اجراي الگوريتم، مي توان جواب مناسب را با هزينه کمي بدست آورد. رو شهاي گوناگوني براي تنظيم اين واريانس وجود دارد که دو روش يک پنجم موفقيت و خودتطبيقي از معروفترين رو شهاي آن محسوب مي گردند. در روش خود تطبيقي که خود با توجه به روشهاي متفاوت منجر به توليد الگوريتمهاي متفاوت استراتژي تکاملي مي گردد، پارامترهاي جهش خود به عنوان عضوي از جمعيت در حال تکامل محسوب شده و به صورت خودکار در طي اجراي الگوريتم مورد اصلاح قرار مي گيرند. اين موضوع با توجه به ماهيت الگوريتمهاي تکاملي که در ابتداي فعاليت مي توانند به سرعت به جوابهاي محلي نزديک شده و در انتها نيازمند افزايش دقت تخمين مي باشند، داراي اهميت بسزايي است.
معرفي الگوريتمهاي استراتژي تکاملي ارزيابي شده
استراتژ يهاي تکامل ارزيابي شده ، مشتمل بر چهار استراتژي کلاسيک مي باشند که با توجه به نحوه ي تطبيق واريانس نويز مورد استفاده براي جهش از يکديگر تفکيک مي گردند. هدف استفاده از استراتژي تکاملي بدست آوردن مقادير متغييرها براي مينيمم يا ماکزيمم کردن يک تابع ارزيابي است. اين عمليات مي تواند در توابعي با ابعاد گوناگون و با استفاده از انواع جمعيت ها صورت پذيرد. خصوصيات الگوريتمهاي استراتژي تکاملي به صورت خلاصه عبارتند از:
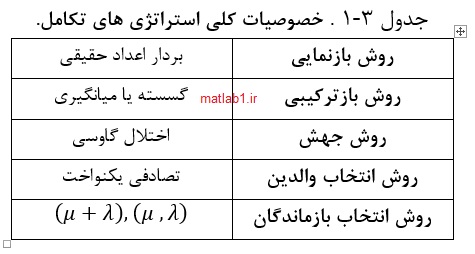
جدول 3 1 . خصوصيات کلي استراتژي هاي تکامل.
روش بازنمايي در استراتژي هاي تکاملي
بازنمايي مساله در استراتژيهاي تکاملي با استفاده از برداري از اعداد حقيقي صورت مي پذيرد که طول اين بردار متناسب با ابعاد مساله مي باشد. وابسته به نوع استراتژي پارامترهايي نيز به اين بردار اضافه مي شوند و در نتيجه براي هر نوع از استراتژيهاي تکاملي بردار بازنمايي متفاوتي مورد استفاده قرار مي گيرد.
انواع بازترکيب در استراتژي هاي تکاملي
براي بازترکيب از چند روش استفاده مي شود که وابسته به نوع استراتژي و مساله انتخاب مي شود. اين روش ها عبارتند از:
انتخاب تنها يک فرزند. اين روش در مدل استراتژي تکاملي ES (1+1) کاربرد دارد. چرا که در اين مدل هر والد تنها يک فرزند را نتيجه خواهد داد و در نتيجه امکان بازترکيبي وجود نخواهد داشت.
روش ميانگين گيري محلي: که در طي آن دو والد به صورت ثابت براي تمامي ژن ها انتخاب شده و فرزندان با استفاده از روابط زير بدست مي آيند:

در روابط فوق ضريب α بين صفر و يک است که مي تواند به سه طريق ثابت، تصادفي، يا متناسب با زمان تعيين شود. xi و yi معرف دو ژن همتراز از دو والدي هستند که به صورت ثابت براي تمامي ژن ها انتخاب شده اند. yi’ و xi’معرف مقادير جديد براي ژن ها پس از بازترکيب مي باشد.
روش ميانگين گيري عمومي: مشابه روش قبل است با اين تفاوت که براي هر ژن دو والد به صورت تصادفي انتخاب مي گردد. در اين روش ضريب α همانند روش قبل تعيين شده وa_n معرف والدين انتخابي براي ژن n ام است. در نتيجه براي هر ژن در هنگام بازترکيب از والدين متفاوتي استفاده خواهد شد.
رابطه مربوط به اين روش به صورت زير مي باشد:

روش انتخاب بازماندگان در استراتژي هاي تکاملي
روش انتخاب بازماندگان مي تواند يکي از دو روش(μ+λ) و (μ ,λ) صورت پذيرد. بدان معني که به ترتيب بازماندگان از ميان مجموع والدين و فرزندان انتخاب شوند يا تنها از ميان فرزندان انتخاب شوند. به طور کلي در صورتي که روش انتخاب از نوع (μ+λ) انتخاب شود از روش تورنمنت براي انتخاب بازماندگان استفاده مي شود و در صورتي که از (μ ,λ) استفاده شود مي بايست از روش انتخاب مبتني بر شايستگي بهره برداري گردد. به صورت کلي مي توان گفت در استراتژيهاي تکاملي بالاخص استراتژيهايي که از خود تطبيقي بهره برداري مي کنند ، روش (μ ,λ) بهتر از روش (μ+λ) عمل مي کند چرا که اين روش موجب فراموشي مقادير قبلي است.
روش جهش در استراتژي هاي تكاملي
جهش در استراتژيهاي تکاملي از اساسي ترين بخشهاي الگوريتم است و تقريباً تمامي استراتژيهاي تکاملي مبتني بر جهش مي باشند. براي جهش از پارامتر يا پارامتر هايي استفاده مي شود که اين پارامترها مي توانند علاوه بر روشهاي معمول به صورت تطبيقي تغيير نمايند. تمامي پارامتر هاي پيش گفته پارامتر هايي داخلي هستند که مي توانند در انواع استراتژ يهاي تکاملي مورد استفاده قرار گيرند. با اين حال آنچه که موجب گوناگوني اين الگوريتمها مي شود نحوه ي تطبيق پارامترهاي جهش مي باشد. به صورت کلي مي توان رو شهاي تطبيق را به صورت زير دسته بندي نمود:
• عدم تطبيق و استفاده از واريانس ثابت. اين روش در استراتژيهاي تکاملي کارايي ندارد چرا که اساس اين الگوريتمها بر جهش استوار است و در صورتي که واريانس نويز گاوسي مورد استفاده در جهش در طول اجراي الگوريتم اصلاح نشود تضميني براي رسيدن به جواب و همگرايي وجود نخواهد داشت.
• تطبيق متناسب با زمان. در اين روش، واريانس انتخابي ، متناسب با زمان اجراي الگوريتم کاهش مي يابد تا درابتداي کار امکان افزايش سرعت در رسيدن به پاسخ وجود داشته باشد و در انتها دقت در رسيدن به جواب مطلوب افزايش يابد. اين روش خود مبتني بر دو روش خطي و نمايي است. در روش خطي از رابطه زير براي تعيين مقدار واريانس استفاده مي شود. در اين رابطه N معرف حداکثر تعداد مجاز اجراي الگوريتم يا توليد نسل بوده و t معرف مرتبه ي اجراي الگوريتم يا شماره نسل مي باشد. اعداد انتخابي براي حداقل و حداکثر سيگما نيز خود مي توانند در نحوه ي رفتار تطبيق کننده تاثير داشته باشند.
روند کلي استراتژي هاي تکاملي
به طور کلي در تمامي استراتژيهاي تکاملي اولين قدم توليد جمعيت اوليه مي باشد. براي اين منظور با توجه به نوع استراتژي انتخابي ، برداري به طول ابعاد مساله از اعداد تصادفي در دامنه ي مساله ايجاد نموده و درصورت لزوم بردار پارامترهاي مساله نيز توليد و مقدار دهي اوليه مي شود. سپس مراحل اجراي الگوريتم به صورت زير پيگيري مي شود:
ابتدا مقدار تابع با توجه به مقادير اوليه محاسبه مي گردد.
در صورتي که تعداد والدين ( μ ) بيش از يکي باشد عمليات بازترکيبي بر اساس روش انتخاب شده صورت گرفته و کروموزوم جديدي تشکيل مي شود.
به تعداد لازم ، λ فرزند با استفاده از عمليات جهش بر اساس نوع الگوريتم انتخابي توليد مي گردد. در صورتي که فرزندان در بازه ي مساله نباشند مي توان به يکي از رو شهاي : توليد مجدد همه فرزندان، توليد مجدد فرزندان خارج از بازه، قرينه سازي نسبت به مرز بازه ي نزديک و انتخاب حداقل يا حداکثر بازه ي نزديک، آنها را اصلاح نمود.
بازماندگان بر اساس روش انتخابي (μ+λ) يا (μ ,λ) انتخاب مي گردند.
تا زماني که شرط خاتمه برقرار نشده است عمليات از مرحله ۲ تکرار مي شود.
.
کدهای اماده الگوریتم استراتژی تکاملی به همراه یک فیلم آموزشی فارسی از این الگوریتم توسط گروه ایران متلب آماده شده است که شما می توانید تقاضای این کد و فیلم آموزش فارسی را از برای ما ارسال کنید.
بعد از واریز هزینه کدها آماده متلب MATLAB ، الگوریتم استراتژی تکاملی به همراه یک فیلم آموزشی فارسی برای شما ارسال و می توانید آنها را دانلود کنید و در پروژه یا پایان نامه خود استفاده کنید.

بسیار عالی و آموزنده بود. سپاسگزارم
سلام وقت بخیر
هزینه آماده سازی کد متلب الگوریتم استراتژی تکاملی برای مسئله مکانیابی-مسیریابی چقدر می باشد؟
سلام
من کد و فیلم آموزشی استراتژی تکاملیES رو میخواستم
متاسفانه وقتی روی لینک سفارش کلیک میکنم کد و فیلم آموزشی الگوریتم تفاضل مرکزیDE برای دانلود قرار داده شده است
امکانش هست فیلم آموزشی و کد ES رو قرار روی سایت قرار بدهید؟؟
طفا کد و فیلم آموزشی استراتژی تکاملی (ES ) را در سایت قرار دهید!!
تشکر