الگوريتم جستجوي هارموني يك الگوريتم تكاملي بنا شده بر مبناي عملكرد سازهاي موسيقي است[33][34] . اين الگوريتم با مفهومي ساده و تعداد پارامتر هاي كم مي باشد. الگوريتم جستجوي هارموني بر اساس عملکرد موسيقيدانان براي ايجاد يک ملودي جديد و هماهنگي نت ها از نظر فرکانس و طول موج آنها استوار است.
اين الگوريتم به صورت موفقيت آميزي براي انواع مسائل دنياي واقعي شامل مسئله فروشنده دوره گرد، بهينه سازي پارامتر هاي مدل رود خانه، طراحي شبكه هاي خط لوله و طراحي سازه ها بكار گرفته شده است گام هاي الگوريتم فوق عبارتند از:
گام اول: تعيين مقادير ابتدايي پارامتر هاي الگوريتم و مسئله
گام دوم : تعيين مقادير ابتداي حافظه هارموني
گام سوم: بهبود هارموني جديد
گام چهارم: بروزدرآوري حافظه هارموني
گام پنجم : تست قاعده توقف
حافظه هارموني ماتريسي است كه از راه حلهاي ممكن و غير ممكن تشكيل شده است .
پارامترهاي اين الگوريتم عبارتند از :
ميزان فضاي حافظه HMS
نرخ حافظه هارموني HMCR
نرخ اصلاح هارموني PAR
پارامتر شبيه سازي ECR
در اين روش با توجه به توصيه هاي محققين قبلي وگراف تحليل حساسيت شکل3-2 ،براي پارامتر ها مقادير مناسب تعيين مي شود وسپس براساس کد نويسي هاي برنامه، بهينه سازي انجام مي گيرد.
موسيقي يک پديده مصنوعي آرام بخش است که توسط انسان و طبيعت توليد ميشود، هارموني در موسيقي اصطلاحا به اجراي نتهاي متفاوت به صورت همزمان ميگويند که در نهايت تبديل به آهنگي موزون و زيبا از نظر شنيداري ميشود. الگوريتم جستجوي هارموني به عنوان يکي از روشهاي جديد بهينه سازي فراکاوشي که از پديده موسيقي الهام گرفته، معرفي شده است. مفاهيم پايه اي الگوريتم جستجوي هارموني براي اولين بار توسط يک فيلسوف يوناني و رياضيدان معروف، فيثاغورث پيشنهاد شد.
بعدها محققان زيادي در اين پديده تحقيق کردند. جين فليپ آهنگساز و موسيقيدان فرانسوي که در سالهاي 1764-1683 مي زيست، تئوري هارموني کلاسيک را ثابت کرد. تيرو موسيقيدان فرانسوي در سال 1977 تاريخچه جاز 2را در آمريکا به سنديت در آورد.
در کارهاي موسيقي جستجوي بهترين موقعيت (هارموني خارق العاده) به وسيله تخمين زيباشناسي تعيين ميشود. معمولا دًر الگوريتم هاي بهينه سازي کلاسيک، بهترين موقعيت (بهينه سراسري، مينيمم هزينه و ماکزيمم سود يا راندمان) به وسيله ارزيابي توابع هدف تعيين ميشود، در صورتي که تخمين زيباشناسي به وسيله ارزيابي توابع هدف که از مقادير ثبت شده ي مولفه ي متغيرها بدست مي آيد، انجام مي گيرد. در موسيقي، به منظور دستيابي به بهترين اجرا هر تمرين با تمرين قبل مورد مقايسه قرار مي گيرد. در حالي که در بهينه سازي ، توابع هدف در هر تکرار، نسبت به تکرارهاي قبل مقايسه مي شود.
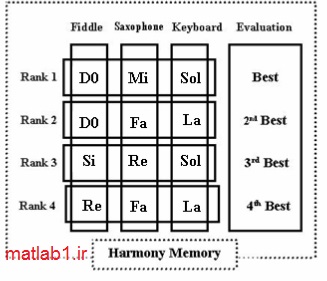
در شکل بالا ساختار حافظه هارموني با ترکيبي ، از سه ساز در يک ارکستر سه نفره متشکل از فيدل و ساکسافن و کيبورد مورد بررسي قرار مي گيرد. در ابتدا حافظه، توسط هارمونيهاي تصادفي (Re,Fa,La) و (Si,Re,Sol) ، (Do,Fa,La) ، (Do,Mi,Sol) پر شده و سپس به وسيله تخمين زيباشناسي ، هارمونيها ، مرتب شده اند.
به طور کلي فرآيند بهينه سازي جستجوي هارموني در پنج گام خلاصه ميشود.
گام اول: معرفي مسئله بهينه سازي و پارامترهاي الگوريتم،
گام دوم: توليد حافظه هارموني اوليه،
گام سوم: اصلاح هارموني جديد،
گام چهارم: جديد کردن حافظه هارموني
گام پنجم: بررسي معيار توقف است.
هر يک از گامها به طور کامل در زير شرح داده شده است.
گام اول: معرفي مسئله بهينه سازي و پارامترهاي الگوريتم
در مدل بهينه سازي اين پايان نامه محـدوده مجـاز براي هر متغير تصميم به صـورت 100≤R(t)≤0 کـه 0و100 به ترتيب محـدوده پـايين و بـالاي هـر متغيـرتصميم مي باشد. در ايـن گـام يـک سـري پارامترهـايي مخصوص الگوريتم جستجوي هارموني ازجمله: انـدازه حافظه هارموني (HMS) که تعداد بردارهـاي جـواب رادر حافظـه هـارموني نـشان مـي دهـد، سـرعت بررسـي حافظه هارموني HMCR))، سـرعت تنظـيم قطعـات PAR))و ماکزيمم تعداد تکرارها NI)) يـا شـرط توقـف وارد مي شود.
گام دوم: توليد حافظه هارموني اوليه
در گام دوم به صورت تصادفي از محدوده مقادير ممکن متغير تصميم، يک حافظه هارموني به صورت زير تشکيل ميشود:

که F(R^1) مقدار تابع هدف بدست آمده به ازاي بردار اول و HM ماتريس حافظه هارموني است.
گام سوم: اصلاح هارموني جديد
در اين گام با استفاده از سه مکانيزم انتخاب تصادفي، بررسي حافظه و سرعت تنظيم قطعات يک هارموني جديد به صورت

توليد مي کنند، البته بايد متغيرهاي تصميم توليد شده در اين مرحله در محدوده مجاز واقع شوند.
HMCR که بين مقدار صفر و يک تغيير مي کند. سرعت انتخاب از مقادير مرتب شده در حافظه هارموني است در حالي که 1-HCMR سرعت انتخاب تصادفي از محدوده مجاز است.

به عنوان مثال، اگر HMCR برابر 0.85 باشد، الگوريتم با احتمال 85 درصد بردار جديد را از بين بردارهاي مرتب شده در حافظه هارموني انتخاب ميکند و با احتمال 15 درصد بردار جديد به صورت تصادفي در محدوده مجاز انتخاب ميکند.
براي هر بردار جديد بدست آمده بايد امتحان شود که آيا لازم است تنظيم قطعات بر روي آن انجام شود؟ اگر جواب بله بود با احتمال PAR همسايه هاي بالا و پايين نقطه بدست آمده را مورد بررسي قرار مي دهند:
![]()
اما اگر جواب منفي باشد، با احتمال 1-PAR کاري انجام نمي دهد. bw فاصله اختياري براي پهناي بررسي و rand( ) اعداد تصادفي بين صفر و يک هستند.
گام چهارم: جديد کردن حافظه هارموني
اگر هارموني جديد توليد شده بهتر از بدترين هارموني موجود در حافظه هارموني باشد، جايگزين آن در حافظه مي شود و به اين ترتيب هارموني بدتر از حافظه خارج مي شود. اما اگر هارموني جديد بهتر از بدترين هارموني موجود در حافظه باشد در اين صورت بدون هيچ جايگزيني الگوريتم وارد تکرار بعدي مي شود.
گام پنجم: بررسي معيار توقف
گام سوم و چهارم آنقدر تکرار ميشود تا شرط توقف ارضا شود. به اين ترتيب آخرين بردار بدست آمده در الگوريتم جواب مسئله است.
.
.
کدهای اماده الگوریتم جستجوي هارموني به همراه یک فیلم آموزشی فارسی از این الگوریتم توسط گروه ایران متلب آماده شده است که شما می توانید تقاضای این کد و فیلم آموزش فارسی را از برای ما ارسال کنید.
بعد از واریز هزینه کدها آماده متلب MATLAB ، الگوریتم جستجوي هارموني به همراه یک فیلم آموزشی فارسی برای شما ارسال و می توانید آنها را دانلود کنید و در پروژه یا پایان نامه خود استفاده کنید.
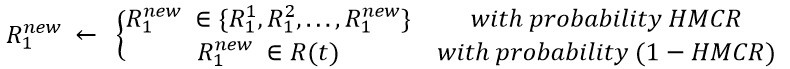
آیا از این کد میشه برای بهینه سازی تعداد دیزل ژنراتورهای نیروگاه استفاده کرد؟
بله از این کد متلب میشه برای هر نوع مسئله بهینه سازی استفاده کرد.
سلام خیلی مفید بود
دستتون درد نکنه
من رشتم مهندسی پزشکیه. این فیلم و کد به درد من میخوره؟
این محصول برای هر رشته ای که بخواهد از الگوریتم جستجوی هارمونی استفاده کند، مناسب است.
خیلی خوب بود
نتایج الگوریتم جستجوی هارمونی با چه الگوریتمی مشابه هست؟
سلام برای تهیه این کد از کجا باید اقدام کنیم ؟
سلام
با پشتیانی تماس بگیرید.