نظریه گراف

تاریخچه

تعداد علومی که بتوان به وضوح زمانی را برای شروع آنها تعیین کرد زیاد نیست. نظریه گراف که یکی از بنیان های ریاضی دانش شبکه ها است در سال 1736 میلادی توسط اویلر[1]، ریاضی دان سوئیسی در پی حل معمای پل های کونیگزبرگ[2] مطرح کرد. این پل های هفت گانه (همانطور که در شکل زیر مشاهده می‌شود،) یک جزیره و سه ساحل مجاور آن را به یکدیگر مرتبط می‌ساختند. معما از این قرار بود که آیا کسی می‌تواند بدون عبور مجدد از یک پل، از تمام پل ها عبور کند؟ این معما که تا دو سال بدون پاسخ باقی مانده بود، سرانجام توسط اویلر با مدل سازی مسئله به صورت یک گراف، حل شد (6).

[1] Euler

[2] Puzzle of Königsberg’s bridges

در سال ۱۸۴۷، گوستاو کیرشهف نوع خاصی از گراف‌ها به نام درخت را مورد بررسی قرار داد. کیرشهف این مفهوم را هنگام تعمیم قوانین اهم برای جریان الکتریکی در کاربردهایی که حاوی شبکه‌های الکتریکی بودند به‌کار گرفت. ده سال بعد، آرتور کیلی همین نوع گراف را برای شمارش ایزومرهای متمایز هیدروکربنهای اشباع شده ی مولکول C_nH_2n+2 به‌کار برد.

در همین دوران شاهد ظهور دو ایده ی مهم دیگر در صحنه هستیم. ایده ی اول حدس چهار رنگ بود که نخستین بار توسط فرانسیس گوثری در حدود سال ۱۸۵۰ مورد تحقیق قرار گرفت. این مسئله سرانجام در سال ۱۹۷۶، توسط کنث ایپل و ولفگانگ هیکن و با استفاده از یک تحلیل رایانه‌ای پیچیده حل شد. ایده ی مهم دوم، دور همیلتونی بود. این دور به افتخار سر ویلیام روآن همیلتون نامگذاری شده است. او این ایده را در سال ۱۸۵۹ برای حل معمای جالبی حاوی یال‌های یک دوازده وجهی منتظم به‌کار گرفت. یافتن جوابی برای این معما چندان دشوار نیست ، ولی ریاضیدانان هنوز در پی یافتن شرایطی لازم و کافی هستند که گراف‌های بدون جهت حاوی مسیر یا دورهای همیلتونی را مشخص کنند.

پس از این کارها تا بعد از سال ۱۹۲۰ فعالیت اندکی در این زمینه صورت گرفت. مسئله ی مشخص کردن گراف‌های مسطح را کازیمیر کوراتوفسکی، ریاضیدان لهستانی، در سال ۱۹۳۰ حل کرد. نخستین کتاب درباره ی نظریه ی گراف در سال ۱۹۳۶ منتشر شد. این کتاب را ریاضیدان مجارستانی، دنش کونیگ، که خود محقق برجسته‌ای در این زمینه بود، نوشت. از آن پس فعالیت‌های بسیاری در این زمینه صورت گرفته و کامپیوتر نیز در چهار دهه ی اخیر به یاری این فعالیت‌ها آمده است (7).

مفاهیم اولیه

سيستم های پيچيده نگاهی نو به پديده هایي است که به علت ارتباط بين اجزای آن و همچنين ارتباط با ديگر پديده ها، از پيچيدگی بالايی برخوردارند و رفتار جمعی متفاوتی بروز می‌دهند. بدين معنی که با مطالعه تک تک اجزای یک سيستم پيچيده نمی‌توان به رفتار جمعی آن دست يافت.

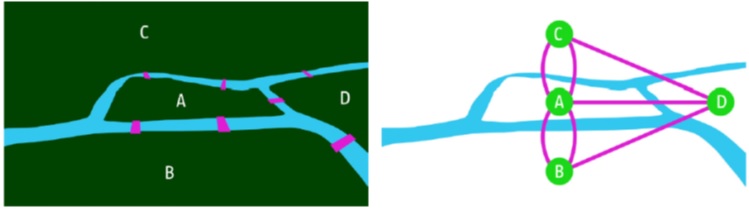
اگر بخواهیم یک سیستم پیچیده را بهتر درک و توصیف کنیم، نیاز داریم که آن را به صورت یک شبکه نمایش دهیم. به بیان ساده، یک شبکه یا گراف شامل اجزایی به نام گره[1] یا رأس[2] است که ارتباط مستقیم میان آنها توسط پیوندها[3] و یا یال ها[4] مشخص می‌شود. این نوع نمایش زبان مشترکی را برای توصیف پدیده های مختلف ارائه می‌دهد (8).

[1] Node

[2] Vertex

[3] Link

[4] Edge

در ادامه به چند تعریف و مفهوم پایه در زمینه شبکه ها و گراف ها می‌پردازیم (8):

تعداد گره ها (یا رأس ها): به مجموع تعداد اجزای یک گراف گفته می‌شود و معمولا با حرف N یا V نمایش داده شده و آن را اندازه شبکه یا گراف نیز می‌نامند.

تعداد پیوند ها (یا یال ها): به مجموع ارتباطات بین اجزای یک گراف (گره ها) گفته شده و معمولا با حرف L  یا E نمایش داده می‌شود.

گراف جهت دار[1]: به گرافی که یال های آن جهت داشته باشند جهت دار و در غیر این صورت بدون جهت[2] می‌گویند. به عنوان مثال، گراف جاده های شهری جهت دار است، زیرا در آن جهت تردد وسایل نقلیه نیز در نظر گرفته می‌شود.

گراف وزن دار[3]: به گرافی که یال های آن دارای وزن باشند وزن دار و در غیر این صورت بدون وزن[4] می‌گویند. به عنوان مثال، گراف نشان دهنده ارتباط بین کلمات وزن دار است و در آن کلماتی که از نظر مفهومی شباهت بیشتری به یکدیگر دارند با وزن بیشتری به یکدیگر متصل شده اند.

درجه گره[5]: به تعداد پیوندهایی که یک گره با سایر گره ها دارد درجه آن گره گفته شده و معمولا با حرف K نمایش داده می‌شود.

میانگین درجه[6]: به میانگین تمام درجات گره های یک گراف، میانگین درجه آن گفته می‌شود.

توزیع درجه[7]: به توزیع احتمالی که بتوان به وسیله آن پراکندگی درجه گره های یک گراف را توصیف کرد، توزیع درجه آن می‌گویند. به بیان دیگر، اگر گره ای به صورت تصادفی از گراف انتخاب شود، این نمودار بتواند نشان دهد که این گره با چه احتمالی درجه خاصی (مثلا درجه 2) را خواهد داشت.

تصویر 9: دو نمونه گراف و نمودار توزیع درجه آنها

 

گراف کامل[8]: به گرافی که در آن هر گره به تمام گره های دیگر متصل باشد گراف کامل می‌گویند.

تصویر 10: یک گراف کامل

 

گراف تنک (یا خلوت)[9]: به گرافی که تعداد یال های آن خیلی کمتر از گراف کامل نظیرش باشد، گراف تنک می‌گویند.

[1] Directed Graph

[2] Undirected Graph

[3] Weighted Graph

[4] None Weighted Graph

[5] Node Degree

[6] Average Degree

[7] Degree Distribution

[8] Complete Graph

[9] Sparse Graph