روشهای چند رزولوشنی به طور عمیقی به پردازش تصویر و ماشین بینایی و محاسبات علمی مرتبط هستند. تبدیل کرولت یک تبدیل چند جهتی چند مقیاسی است. تبدیل کرولت بیان غیر وفقی بهینه از لبه ها می باشد. از این تبدیل در پردازش تصویر و ویدئو و اکتشاف لرزه ای و مکانیک سیالات و شبیه سازی معادلات دیفرانسیل جزیی و سنجش فشرده استفاده می شود.
تبدیل کرولت یکی از زمینه های مورد علاقه می باشد زیرا خیلی از مشکلات تبدیل های دیگر مثل تبدیل ویولت را به طور موثرتری برطرف می کند.
این تبدیل برای اشیا با انحنا (curve) مناسب می باشد و نام این تبدیل هم از همین خصوصیت آن گرفته شده است. در سال 1999 توسط Candès و Donoho معرفی شد.
نرخ های تقریب (Approximation Rates) :
فرض کنید یک شی در فضای [0,1] در [0,1] قرار دارد . دقت تبدیل فوریه و تبدیل ویولت و تبدیل کرولت در بیان این شی در قسمت زیر نشان داده شده است :
تبدیل فوریه Fourier Transform :
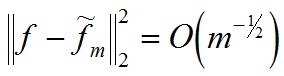
تبدیل ویولت Wavelet Transform :
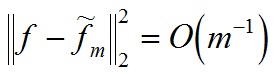
تبدیل کرولت Curvelet Transform :

همانطور که مشاهده می فرمایید خطای بین شی و بیان تبدیل یافته آن در تبدیل کرولت کمتر از دو تبدیل دیگر است.
عدم پیوستگی در منحنی و نقطه
Point and Curve Discontinuities
عدم پیوستگی نقطه ای در تبدیل فوریه بر روی همه ضرایب آن تاثیر می گذارد. لذا تبدیل فوریه نمی تواند با عدم پیوستگی نقطه ای به خوبی رفتار کند. اما تبدیل ویولت به خوبی عدم پیوستگی نقطه ای را بیان می کند و تنها تعداد کمی از ضرایب آن دستخوش تغییر می شوند.
عدم پیوستگی بر روی یک منحنی ، تمامی ضرایب تبدیل ویولت را تغییر دهد لذا تبدیل ویولت نمی تواند در اشیا با عدم پیوستگی در منحنی به خوبی رفتار کند. اما تبدیل کرولت طراحی شد تا عدم پیوستگی در منحنی را بیان کند و تنها تعداد کمی از ضرایب آن دستخوش تغییر شود.
بنا به درخواست کاربران فهیم سایت ایران متلب ، فیلم آموزشی برنامه نویسی تبدیل کرولت در متلب برای استفاده آماده شد.
این فیلم آموزشی اختصاص به طریقه کدنویسی و برنامه نویسی و کار با تبدیل کرولت در متلب دارد. در ابتدا تئوری مختصری از روشهای موجود صحبت می شود. اختلاف این روشها با هم و مزیت هر کدام بیان می شود. سپس توابع متلب مختص تبدیل کرولت به تفضیل معرفی می شوند. در انتها چندین مثال برنامه نویسی متلب آورده شده است.
پیش نمایش :
تصاویری از این فیلم آموزشی :






