جعبه ابزار PDE از نرم افزار Matlab محيطي قدرتمند براي تجزيه و تحليل معادلات با مشتقات جزيي IBVP در فضاي دو بعدي و زمان ارائه مي كند. در اين جعبه ابزار معادلات با روش اجزاء محدود (Finite Element Method) تحليل مي گردند.
كمترين نياز ما فرموله كردن مسائل PDE (از جمله ترسيم خصوصيات، نوشتن شرايط مرزي و معادلات با مشتقات جزيي) است. براي شروع كار پس از اجراي Matlab در خط فرمان تايپ كنيد:
pdetool
با اجراي اين دستور محيط گرافيكي براي حل PDE باز مي شود. اين محيط به شكل زير می باشد:
چه مسايلي را مي توان با اين ابزار حل نمود؟
معادلات PDE به عنوان مدل رياضي پديده هاي مختلف استفاده مي شود. براي نمونه، معادلات بيضوي و هذلولوي را مي توان در حالت هاي دائم و غير دائم انتقال حرارت، جريان داخل خلل و فرج هاي نامنظم و براي جريان پتانسيل به كار برد.
به اين منظور مراحل زير را انجام مي دهيم:
– استفاده از GUI براي ايجاد موضوع
– ايجاد هندسه با CSG
– تعريف شرايط مرزي
– تعيين ضرايب قابل تغيير و مسئله PDE
– مش بندي كامل
– مشخص كردن سيستم حل كننده با تغيير متغيرهاي وابسته
– شبيه سازي خواص تعريف شده
پروسه حل معادلات PDE با MATLAB كه از روش Finite Elements Method استفاده مي كند، شامل مراحل زير است:
- تعريف كردن هندسه موضوع (draw mode)
- (boundry condition mode) تعريف شرايط مرزي
- انتخاب ضرايب معادله (PDE mode)PDE
- (mesh mode) FEM فيلتر و صلاحديد
- مشخص كردن شرايط اوليه و حلگر (solve mode)PDE
- پس پردازش و حل PDE
معادله پايه جعبه ابزار PDE، معادله ديفرانسيل زير است كه به نام معادله بيضوي ( elliptic ) معروف است.
تعريف يك مسئله PDE
براي شروع همان طور كه قبلا اشاره شد، از GUI يا رابط گرافيكي استفاده مي كنيم. مسئله اي كه ما قصد داريم آن را حل كنيم، معادله پواسون مي باشد. هندسه اين مسئله به صورت quite complex است و شرايط مرزي از نوع ديريخله و نيومن هستند.
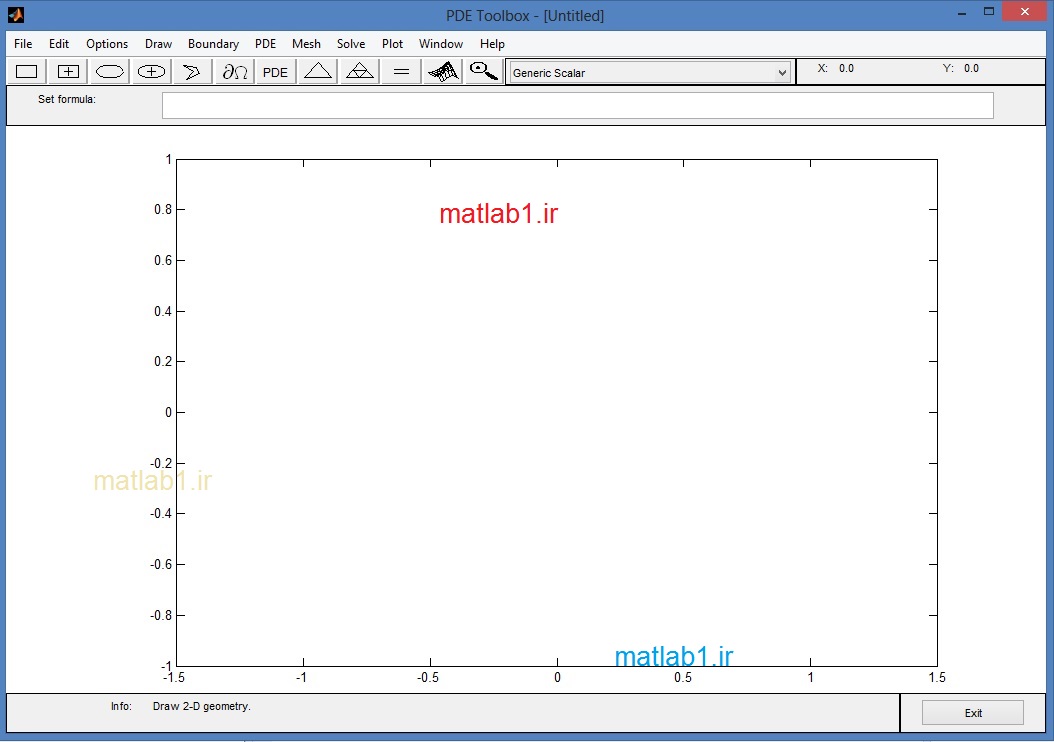
با اجراي Matlab در خط فرمان دستور pdetool را وارد مي كنيم يا از منوي start گزينه Toolbox و سپس گزينه Partial Differential Equation و بعد گزينه PDETool GUI را انتخاب مي كنيم. بعد از لحظاتي GUI به صورت زير ظاهر مي شود:
Grid را از منوي option/grid فعال كنيد. همچنين snap را از منوي options فعال نمائيد. اين گزينه به ترسيم كمك مي كند. اولين مرحله، ترسيم هندسه جسم مورد نظر است. GUI تعدادي از اشكال ساده مانند بيضي، مستطيل، دايره و مثلث را دارد. اين اشكال براي ايجاد ساختار مدل هندسي يا CGS Model به كار مي روند. هر عضو يك برچسب دارد. به عنوان مثال مستطيل اول 1R و دايره اول 1C و … . با انتخاب هر عضو مي توان آن را جابجا كرد. از گزينه هاي copy,cut,clear,delete مي توان ويرايش هاي دلخواه را انجام داد.
براي انتخاب دو يا چند عضو مي توان از shift استفاده كرد. به طور پيش فرض كليه موضوعات با يكديگر
در فيلد ويرايش فرمول جمع مي شوند. (C1+R1+R2+E1)، مي توان مقادير ديگري در اين فيلد وارد كرد، مانند
به منظور ذخيره مدل CSG به عنوان يك M‐File از منوي File گزينه Save As را انتخاب كنيد. حال مي توان شرايط مرزي را تعريف كرد. Boundry Mode را با استفاده از آيكون Ω∂ و يا با انتخاب BoundryMode از منوي Boundry ايجاد مي كنيم.
با Double‐click بر روي تك تك مرزها قسمت انتخاب شده، پنجره محاوره اي BoundryCondition نمايان مي شود. در اينجا نوع شرايط مرزي را انتخاب كرده و به عنوان يك يك عبارت Matlab شرط مرزي خود را اعمال مي كنيد. در حين تغيير شرايط مرزي، شرط نيومان 5 را بر مرزها اعمال كنيد. در پنجره Boundry Condition شرط Neumann را انتخاب مي كنيم و عدد 5‐ را در جلوي پارامتر g وارد مي كنيم. براي اعمال يك يك شرط Neumann خالص مقدار پارامتر q را صفر وارد مي كنيم. روي OK كليك مي كنيم. اين كار را بر روي تك تك مرزهايي كه به رنگ قرمز هستند انجام مي دهيم و پس از اعمال شرايط مرزي روي هر كدام از مرزهاي قرمز، به رنگ آبي در مي آيند.
با كليك بر روي آيكون PDE يا انتخاب PDE Specification از منوي PDE، نوع معادله را مشخص مي كنيم. به عنوان مثال معادله بيضوي . . را انتخاب مي كنيم و ضرايب f=10.0 و a=0 و c=1.0 را وارد مي كنيم.
بالاخره با ايجاد mesh مثلثي از طريق آيكون ∆ يا منوي Mesh>Initailize Mesh، سطح به قطعات مثلثي تقسيم مي شود. اگر نياز به حل دقيقتري داريم، با انتخاب Refine Mesh از منوي Mesh به مش ريزتر و حل دقيقتر و درعين حال زمان بر مي رسيم.
در اينجا روشهاي مختلفي براي ترسيم براي كمك به تصور ما از راه حل وجود دارد. از طريق آيكون
Plot Selection و يا در قسمت Parameters از منوي Plot به پنجره انتخاب نوع ترسيم مي رسيم. انواع متعددي از ترسيم موجودند كه تنظيمات دلخواه خود را انجام داده و خارج مي شويم و يا با انتخاب plot شكل سه بعدي آن نمايش داده مي شود.
نمونه هاي كاربردي
در اين بخش نمونه هاي كاربردي ارائه مي شود. براي مشاهده اين كاربردها از گزينه Application از منوي Option قابل دسترسي هستند.
انتقال حرارت
معادله انتقال حرارت يك معادله سهموي مي باشد كه به صورت زير است:
- ρ چگالي
- يا C ظرفيت گرمايي
- k ضريب انتقال حرارتي
- q نرخ انتقال گرما
- h ضريب انتقال گرماي جابجايي يا همرفتي
- يا دماي خارج برحسب كلوين
با حل اين معادله مي توان توزيع دما T(x,y,z) را به صورت تابعي از زمان به دست آورد.
اين معادله در حالت دائم به يك حالت خاص معادله سهموي ساده مي شود:
بر روي تك تك مرزها دوبار كليك مي كنيم و شرط نيومن محيط اطراف آنرا با شرط Neumann به صورت عايق (g=0) تعريف مي كنيم.
رساناي گرماي دائم و يك بعدي
مسئله دوبعدي شامل يك مربع جاسازي شده به صورت لوزي داخل يك مربع چرخانده شده به اندازه 45 درجه نسبت به اولي مي باشد. مربع داراي خواص ناحيه اي به صورت ضريب انتقال حرارت 10 و چگالي 2 و لوزي داراي مشخصات انتقال گرمايي 4 و ضريب هدايت 2 و چگالي 1 مي باشد. هر دو ناحيه داراي ظرفيت گرمايي يكسان 0.1 مي باشند.
Heat Transfer را از منوي Options>Application فعال كنيد. در منوي Options گزينه Axis limits را انتخاب و محورها را در محدوده 3.5[ 0.5‐] قرار مي دهيم. مربعي به ضلع 3 و يك لوزي بوسيله Draw>Polygon ترسيم كنيد. سپس مطابق اشكال ادامه مراحل را دنبال نمائيد.
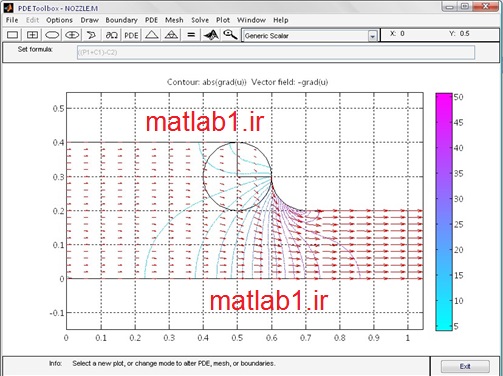
عبور جريان سيال از يك نازل ( لوله همگرا)
اگر سيال غيرچرخشي باشد، بردار سرعتv برحسب گراديان پتانسيل مجهول u بيان مي شود.
مساله را بدين صورت بيان مي كنيم كه رابطه v و u به صورت v=grad(u) مي باشد. چون چگالي ثابت است درنتيجه div(v)=0 مي باشد. پس ما نياز به حل معادله div(grad(u))=0 خواهيم داشت.
ابتدا از منوي Options گزينه هاي Grid و Snaps را فعال مي كنيم. سپس از منوي
حل معادلات دیفرانسیل با مشتقات جزئی PDE در Matlab

سلام.
ببخشید یه سوال داشتم شما پروژه هم میگیرین؟