فیلترهای تطبیقی
فیلتر تطبیقی بلوکی محاسباتی است که تلاش میکند تا بصورت بیدرنگ[2] و تکرار شونده[3] نسبت دو سیگنال را به هم مدل نماید. این فیلترها گاه به صورت تعدادی دستورالعل بر روی یک پردازنده محاسباتی مثل میکروکنترلرها و یا DSP ها پیادهسازی میشوند و گاهی هم به صورت بلوکهای منطقی بر روی FPGA ها و یا قطعات مجتمع VLSI دیده میشوند.
یک فیلتر تطبیقی از چهار بخش اصلی تشکیل میشود:
- سیگنالهایی که توسط فیلتر مورد پردازش قرار میگیرند.
- ساختار فیلتر که رابطۀ بین ورودی و خروجی آن را تعیین میکند.
- پارامترهای فیلتر که مرتباً برای تطبیق با سیستم تغییر میکنند.
- الگوریتم تطبیقی که شیوۀ تغییر پارامترها را با توجه به شرایط سیستم توصیف مینماید.
مقدمهای بر فیلترهای دیجیتال
سالیان زیادی است که فیلترهای دیجیتال به متداولترین کاربرد پردازندههای سیگنال دیجیتال[4] و کامپیوترها تبدیل شدهاند. مهمترین مزیت فیلترهای دیجیتال بر فیلترهای آنالوگ آن است که کد نوشته شده و یا بلوک منطقی ساخته شده برای فیلتر به راحتی قابل تغییر است و میتوان ضرایب فیلتر را طوری تغییر داد که پاسخ فرکانسی و بهره جدیدی از فیلتر بدست آوریم. همچنین در حالی که فیلتر درون سیستم در حال کار است میتوان ضرایب و خصوصیات آن را تغییر داد و به یک فیلتر تطبیقی دست پیدا کرد.
همانند فیلترهای آنالوگ، طراحی فیلترهای دیجیتال در حوزۀ فرکانس به صورت زیر قابل انجام است:
- خصوصیات و ویژگیهای فیلتر را به صورت یک تابع تبدیل در میآوریم.
- پس از اینکه تابع تبدیل فیلتر بدست آمد، میتوان آنرا با استفاده از یک روشهای تکرارشونده[5] و یا تکرار نشونده[6] پیادهسازی نمود.
برای یک فیلتر تکرار شوند، رابطۀ بین ورودی و خروجی به صورت زیر بیان میشود که در آن f(n) دنبالۀ ورودی و g(n) دنبالۀ خروجی فیلتر میباشد.
[1] adaptive filter
[2] real-time
[3] iterative
[5] recursive
[6] non-recursive
پس بنابراین خروجی فعلی نمونۀ g(n) تابعی خواهد بود از ورودیهای گذشته، فعلی و آینده.
اگر فیلتر غیر تکرار شونده باشد خواهیم داشت:
که این رابطه بدین معناست که خروجی فعلی نمونۀ g(n) تنها تابعی خواهد بود از ورودیهای گذشته و ورودیهای فعلی.
روش دیگری برای طبقه بندی انواع فیلتر دیجیتال نیز موجود است. اگر فیلتر دارای پاسخ ضربه با مدت محدود باشد، این فیلتر [1]FIR نامیده میشود. این فیلتر میتواند تکرارشونده و یا غیر تکرارشونده باشد اما معمولاً همواره این نوع فیلترها به صورت غیر تکرارشونده مورد استفاده قرار میگیرند. به همین دلیل است که معادلۀ دیفرنس این فیلتر به صورت زیر بیان میگردد:
[1] Finite-duration Impulse Response
یکی از ویژگیهای مهم فیلتر FIR آن است که لزوماً پایدار است. به دلیل اینکه تمامی قطبهای تابع تبدیل آن در z=0 هستند که درون دایرۀ واحد قرار میگیرند.
حالت عمومیتر معادلۀ دیفرنس برای یک فیلتر دیجیتال به صورت زیر است:
از تابع تبدیل بالا مشخص است که طول نامحدود دارد، به همین دلیل به این گونه از فیلترها، فیلترهای با پاسخ ضربه با طول نامحدود[1] یا IIR میگویند.
ذکر این نکته اهمیت دارد که بیان FIR و یا IIR بودن فیلتر، نوع آن را مشخص میکند، در حالی که تکرارشونده و یا غیرتکرار شونده بودن آن، به روش تحقق[2] فیلتر اشاره مینماید. البته، معمولاً در فیلترهای دیحیتال، غیر تکرار شونده و FIR بجای هم و تکرار شونده و IIR هم به جای هم استفاده میشوند.
[1] Infinite Impulse Response
[2] realization method
پیادهسازی فیلترهای دیجیتال
ماهیت فیلترهای دیجیتال به گونهای است که پیاده سازی آن بر روی پردازندهها به سادگی قابل انجام است. برای مثال خروجی یک فیلتر FIR مرتبه دوم به صورت زیر بیان میشود:
به طریق مشابه، برای یک فیلتر FIR به طور کلی خواهیم داشت:
که در اینجا P مرتبه فیلتر را نشان میدهد.
این فیلتر از تعدادی ضریب و مقادیر ورودی تشکیل شده است. برای محاسبۀ خروجی فیلتر در هر زمان، کافی است که مقادیر ورودی را در ضرایب مربوطه ضرب کرده و مقادیر بدست آمده را با هم جمع کنیم. بهترین روش برای نگهداری اطلاعات جهت شیفت دادن در هر سیکل نمونهبرداری، استفاده از بافر مدور[1] است. به نحوی که شروع اطلاعات با یک نشانگر[2] مشخص میگردد و اطلاعات قبلی به ترتیب از آن نقطه در جهت عقربههای ساعت بار میشوند. وقتی یک نمونۀ جدید دریافت میشود، در محل x(n) قرار میگیرد و زیرروال فیلتر از همان x(n) آغاز میشود و با ضرب مقادیر ورودی در ضرایب مربوط به هر کدام ادامه پیدا میکند. پس از محاسبۀ خروجی، نشانگر در جهت عقربههای ساعت یک واحد جابجا شده و سیستم منتظر ورودی بعدی میماند. همچنین همواره قدیمیترین داده ورودی، پس از محاسبۀ هر خروجی از زنجیرۀ تأخیر بیرون انداخته میشود. با این توصیفات، این بافر مدوری که از آن صحبت میکنیم، در واقع یک FIFO[3] است.
بافر مدور در حالت ایدهآل قابل پیادهسازی است. چرا که هر پردازندهای فضای حافظۀ خطی دارد. یعنی از آدرس 0 شروع شده و به بالاترین آدرس مثلاً XXXX میرسد. بنابراین اگر بخواهیم دادهای را به انتهای حافظه انتقال دهیم، یا با خطا روبرو میشویم و یا اطلاعاتی را از دست خواهیم داد. پس برای پیاده سازی آدرس دهی خطی و یا همان بافر مدور از جابجایی دادهها استفاده میکنیم.
[1] circular buffer
[2] pointer
[3] First In, First Out
مقدمهای در مورد فیلترهای تطبیقی
فیلترهای تطبیقی در مواردی بیشترین استفاده را دارد که پارامترهای سیستم و یا وضعیت سیگنالها در حال تغییر هستند و فیلتر باید طوری تنظیم شود که ای تغییرات را جبران نماید. در فیلترهای FIR و IIR معمولی فرض بر این است که پارامترهایی از فرآیند که ویژگیهای فیلتر را تعیین مینمایند، معین هستند. ممکن است که پارامترهای فیلتر با زمان هم تغییر پیدا کنند، ولی ماهیت این تغییرات قابل پیش بینی است. در بسیاری از مسائل عملی در مورد پارامتهای سیستم عدم قطعیت، به دلیل تأثیر سیگنالهای غیر قابل پیشبینی و همچنین عدم وجود اطلاعات کافی در مورد سیستم وجود دارد. در این موارد برخی از پارامترها باید در طول زمان تغییر پیدا کنند، ولی طبیعت این تغییرات غیرقابل پیشبینی است. در اینگونه موارد، وجود فیلتری مطلوب است تا از نوعی خود-فراگیری[1] بهره ببرد و بتواند خود را با شرایط فعلی سیستم وفق دهد.
ضرایب یک فیلتر تطبیقی طوری تغییر پیدا میکند تا تغییرات در سیگنالهای ورودی، خروجی و پارامترهای سیستم را جبران نماید. به جای اینکه اینگونه فیلترها صلب باشند، در عوض میتوانند ویژگیهای سیگنالی را فرا گیرند و تغییرات آهسته را دنبال کنند. فیلتر تطبیقی در مواردی که مشخصۀ یک سیگنال معین نیست و یا ویژگیها تغییر میکنند، بیشترین استفاده را خواهد داشت.
[1] self-learning
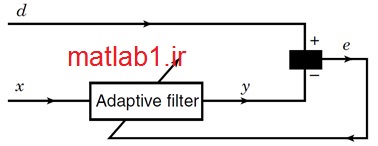
شکل بالا ساختار یک فیلتر تطبیقی ساده را نمایش میدهد که در آن خروجی فیلتر یعنی سیگنال y با سیگنال مطلوب d مقایسه میشود و سیگنال خطا را میسازد که به فیلتر تطبیقی بازخورد پیدا کرده و ضرایب آن را به روز مینماید. روشهای گوناگونی برای پیادهسازی الگوریتم به روز رسانی ضرایب فیلتر وجود دارد که از میان آنها در اینجا به ذکر سه نوع از آنها بسنده میکنیم:
- روش حداقل میانگین مربعات[1]: این نوع از فیلترهای تطبیقی طوری ضرایب فیلتر را تغییر میدهند که میانگین مربعات خطا (تفاضل سیگنال ورودی و سیگنال مطلوب) را به حداقل برساند. این فیلتر از روش نزول شیب تصادفی[2] برای تطبیق استفاده میکند به طوری که تنها با اطلاع از مقدار خطای فعلی ضرایب را تغییر میدهد. این فیلتر در سال 1960 و در دانشگاه استنفورد توسط برنارد ویدرو[3] ابداع گردید.
- روش بازگشتی حداقل مربعات[4]: در این روش ضرایب فیلتر به طور بازگشتی طوری تعیین میگردند که تابع هزینه[5] مربعات خطا به کمترین مقدار برسد. این در تضاد با روشهایی مانند LMS است که در آنها کمترین میانگین مربعات مدنظر است. در روش RLS فرض بر این است که ورودی معین[6] است در حالیکه در روش LMS ورودی تصادفی[7] درنظرگرفته میشود. این روش در مقایسه با همتاهای خود بسیار سریع همگرا میشود ولی حجم محاسباتی زیاد و پیچیدهای را نیز به همراه دارد. شکل زیر شمای کلی یک فیلتر با الگوریتم بهروزرسانی RLS را نشان میدهد.
- روش بلوک چند-تأخیری حوزه فرکانس[8]: این روش در حقیقت پیاده سازی بر پایه بلوک حوزه فرکانس فیلتر LMS است. در این روش فیلتر به صورت بلوکی و در حوزۀ فرکانس بهروز میگردد. به کمک تبدیل FFT سیگنالها به حوزه فرکانس انتقال داده میشوند و در حوزۀ فرکانس فیلتر بر روی آنها اعمال میگردد. به مدد محاسبات بلوکی، حجم محاسبات کاهش چشمگیری پیدا میکند.
[1] least mean squares
[2] stochastic gradient descent
[3] Bernard Widrow
[4] recursive least squares
[5] cost function
[6] deterministic
[7] stochastic
[8] multi-delay block frequency domain
نتیجهگیری و انتخاب الگوریتم مناسب
با توجه به مسائلی که ذکر گردید و با توجه به هدف این پروژه، بهترین انتخاب فیلتری با الگوریتم LMS خواهد بود. چراکه برای پیادهسازی الگوریتم بر روی میکروکنترلر و خروجی محاسبات به صورت بلادرنگ، لازم است تا محاسبات تا حد امکان ساده بوده و حجم محاسباتی نیز متناسب با توان پردازشی موجود باشد. بنابراین در ادامه با انتخاب الگوریتم LMS به ذکر توضیحات و معرفی این روش میپردازیم.
مرور مقالات:
تعداد مقالات مورد بررسی برای این پروژه بیش از 20 مقاله بوده که از این میان تعداد 8 مقاله ارتباط نزدیکی با موضوع داشته و کمک بیشتری را نیز در پیشرفت آن داشته اند که در اینجا به طور خلاصه به هریک از آنها اشاره میکنیم:.
| عنوان مقاله | محل ارائه | سال انتشار |
| Adaptive Notch Filter for EEG Signals Based on the LMS Algorithm with Variable Step-Size Parameter | Conference on Information Sciences and Systems | 2005 |
خلاصه: در این مقاله به طراحی و شبیه سازی یک فیلتر تطبیقی با الگوریتم LMS با پارامتر اندازۀ گام متغیر جهت حذف نویز برق شهر از سیگنال الکروانسفالوگرام پرداخته شده است. مقایسه فیلترهای با اندازۀ گام ثابت و متغیر در این مقاله انجام شده است و برتریهای استفاده از اندازۀ گام متغیر به اثبات رسیده است. از جملۀ آنها میتوان به ایجاد تعادل بین همگرایی، خطای نهایی و پهنای باند طرد[1] اشاره نمود. با استفاده از این روش، دیگر برای پیدا کردن مقدار مناسب پارامتر اندازۀ گام نیازی به سعی و خطا نیست. مزیت بسیار خوب این روش در همگرایی سریع است که در کاربردهای بههنگام[2] مفید است. از دیگر مزایای اشاره شده در این مقاله میتوان به بهینه بودن پهنای باند طرد شده از سیگنال ورودی اشاره نمود که در کاربردهای حذف نویز از سیگنالهای پزشکی که معمولاً دارای مولفههای فرکانس پایین هستند مفید خواهد بود.
| عنوان مقاله | محل ارائه | سال انتشار |
| Design of an Adaptive Filter with a Dynamic Structure for ECG Signal Processing | International Journal of Control, Automation, and Systems | 2005 |
خلاصه: در کاربردهای حذف نویر از سیگنالهای پزشکی استفاده از الگوریتم LMS امری متداول است. اما مشکل در جایی پیدا میشود که مرتبه فیلتر و یا ضرایب آن با توجه به شرایط محیطی و شرایط بیمار به درستی انتخاب نشده باشند. برای رفع این مشکل، در این مقاله الگوریتم جدیدی به نام DSAF[3] ارائه گردیده که در آن مرتبه فیلتر و ضرایب آن با توجه به شرایط محیطی و وضعیت بیمار تغییر پیدا میکند تا بهترین نتیجه حذف نویز را از نظر زمان همگرایی و خطای نهایی بدست دهد. جهت ارزیابی الگوریتم، ارائه دهندگان آن را با استفاده از نرم افزار متلب بر روی چهار سیگنال ECG استاندارد تست کردهاند و نتایج آن را روش مرسوم LMS مقایسه نمودهاند. در نتیجۀ مقایسه، مشاهده میشود که در روش جدید خطای نهایی در کلیۀ شبیهسازیها کاهش پیدا کرده و مرتبه فیلتر نیز به مقدار قابل توجهی کم شده است. ساختار تطبیقی در این الگوریتم در واقع الگوریتم تطبیقی دیگری در دل الگوریتم LMS برای تنظیم مرتبه بهینه فیلتر میباشد.
| عنوان مقاله | محل ارائه | سال انتشار |
| Implementation of the LMSAlgorithm for Noise Cancellation on Speech Using the ARM LPC2378 Processor | Master Thesis, Vaxjo University | 2009 |
خلاصه: همانگونه که در توضیحات الگوریتم LMS به آن اشاره گردید، این الگوریتم در حذف نویز از سیگنالهایی که مرجع نویزِ تغییر شکل پیدا کرده در آنها به نوعی در دسترس است کارآمد خواهد بود. در این پایان نامه، نویسنده با استفاده در الگوریتم LMS نویز موجود در سیگنالهای صوتی را حذف نموده است. بدین منظور از یک میکروفن اضافه در کنار مرجع تولیدکننده نویز استفاده نموده است. سیگنالی که از میکروفن دوم دریافت میشود، مرجع نویز تغییر یافته در دامنه و فاز را به همراه دارد. شبیه سازی ها با نرم افزار متلب انجام پذیرفته است و نتایج نشان داده که نویز به خوبی از سیگنال صوتی حذف گردیده است. نکته مهم در این پایان نامه پیاده سازی الگوریتم بر روی میکروکنترلر بوده است که بیانگر بههنگام بودن سیستم میباشد.
| عنوان مقاله | محل ارائه | سال انتشار |
| Low-Cost, High-Fidelity, Adaptive Cancellation ofPeriodic 60 Hz Noise | University of Texas at Austin | 2008 |
خلاصه: این مقاله به بررسی حذف تطبیقی تویز برق شهر نویز از سیگنالهای پزشکی با استفاده از میکروکنترلر AVR پرداخته شده است. الگوریتم ارائه شده برای حذف نویز همان الگوریتم LMS نرمالیزه شده است که حجم محاسباتی کمی دارد. به دلیل محدودیتهای میکروکنترلر AVR در پردازش سیگنال، در این پروژه بخشی از جمع کنندهها به صورت آنالوگ پیادهسازی شده است. نتایج بدست آمده در تست سخت افزار قابل قبول بوده و نکته مهم در این پروژه کم هزینه بودن آن است. چرا که استفاده از دیگر راهحلها به منظور حذف نویز قطعاً هزینههای بیشتری را به همراه خواهد داشت.
| عنوان مقاله | محل ارائه | سال انتشار |
| Noise Cancellation in ECG Signals usingComputationallySimplified Adaptive FilteringTechniques | Signal Processing: An International Journal | 2009 |
خلاصه: در بخش توضیحات الگوریتم LMS به این موضوع اشاره شد که برای ساده کردن حجم محاسباتی، میتوان از توابع علامتدار استفاده نمود. این مقاله به منظور حذف نویز برق شهر، حرکات ناخواسته و نویز ماهیچهای به روش تطبیقی از سیگنال ECG از الگوریتمهای علامتدار استفاده نموده است و نتایج شبیهسازی بر روی بانک داده MIT-BIH را با الگوریتم قدیمی مقایسه نموده است. نتایج نشان داده است که الگوریتم SRLMS[4] به مراتب بهتر از LMS عمل میکند در حالی که روشهای [5]SLMS و SSLMS[6] از جهت حجم محاسباتی و نسبت سیگنال به نویز خروجی با LMS قابل مقایسه خواهند بود.
| عنوان مقاله | محل ارائه | سال انتشار |
| Noise Removal from Surface Respiratory EMG Signal | World Academy of Science, Engineering and Technology | 2008 |
خلاصه: این مقاله به ارائه روشی برای حذف نویز موجود در سیگنال الکترومایوگرام ارائه نموده است. نویز معرفی شده در این مقاله شامل نویز برق شهر به همراه هارمونیک آن و همچنین نویز حاصل از سیگنال الکتروکاردیوگرام میباشد. الگوریتم استفاده شده در این مقاله روش اصلاح شده LMS استفاده شده است که در آن مرجع برق شهر و هارمونیک آن به روش ریاضی ساخته شده است در حالیکه سیگنال الکتروکاردیوگرام با روش تعقیب انطباق، تقریب زده شده است. نکته مهم در مورد این پروژه عدم استفاده از الکترودهای اضافی برای نمونهگیری از نویز میباشد. مرجع نویز صرفاً به صورت ریاضی و تقریبی استفاده شده است.
| عنوان مقاله | محل ارائه | سال انتشار |
| Performance Study of Various Adaptive FilterAlgorithms forNoise Cancellation in Respiratory Signals | Signal Processing : An International Journal (SPIJ) | 2009 |
خلاصه: حذف نویز از سیگنالهای تنفسی مسئله قدیمی است. الگوریتمهای تطبیقی برای این منظور بسیار کارآمد میباشند. در این مقاله کارآیی روشهای مختلف پیادهسازی الگوریتم LMS برای حذف اینگونه نویزها بررسی شده است. نویز معرفی شده در این مقاله شامل نویز مرجع برق شهر و همچنین نویز حاصل از حرکات هنگام نمونهبرداری است. روشهای LMS، SLMS، SSLMS، BLMS[7] و SRLMS در این مقاله به همراه ضرایب اندازه گام متفاوت مورد بررسی قرار گرفتهاند. نتیجهای که در این مقاله به آن اشاره شده است حاکی از آن است که همواره بین خطای نهایی و ضریب اندازه گام موازنه وجود دارد.
| عنوان مقاله | محل ارائه | سال انتشار |
| POWER LINE INTERFERENCE REMOVAL FROM ELECTROCARDIOGRAM USING A SIMPLIFIED LATTICE BASED ADAPTIVE IIR NOTCH FILTER | IEEE Proceedings – 23rd Annual Conference | 2001 |
خلاصه: در مقاله برخلاف مقالههای پیشین از فیلتر تطبیقی IIR برای حذف تداخل برق شهر استفاده شده است. در این مقاله به مقایسۀ فیلتر ناچ IIR مرتبه دوم و فیلتر تطبیقی IIR مرتبه دوم پرداخته شده است. به دلیل اینکه فرکانس برق شهر را در شبیهسازیها متغیر در نظر گرفتهاند، فیلتر تطبیقی نتیجه مطلوبتری را به همراه داشته است. دقت این الگوریتم از LMS بالاتر بوده ولی به دلیل حجم محاسباتی زیاد، برای پیاده سازی در سیستمهای ارزان قیمت و بیدرنگ مناسب نمیباشد.
[1] rejection bandwidth
[2] real time
[3] Dynamic Structure Adaptive Filter
[4] Signed Regression LMS
[5] Signed LMS
[6] Sign-Sign LMS
[7] Block LMS
ساختارهای تطبیقی:
ساختارهای مختلفی برای فیلترهای تطبیقی معرفی شده است که هر کدام در کاربردهای خاصی مورد استفاده قرار میگیرند:
به منظور حذف نویز[1]: ساختار این فیلتر در شکل 3-2 که اصلاح شده فرم کلی فیلتر تطبیقی شکل 1-2 میباشد مشاهده میگردد. سیگنال مطلوب (d) توسط نویز جمعپذیر[2] (n) که هیچ گونه همبستگی نسبت به هم ندارند تخریب شده است. ورودی فیلتر تطبیقی در اینجا سیگنال n’ است که با نویز موجود در سیگنال اصلی همبستگی و شباهت دارد. معمولاً این سیگنال که توسط محیط تغییر شکل پیدا کرده از منبع تولیدکننده نویز گرفته میشود ولی در کل شبیه به نویز موجود در سیگنال اصلی است. در اینجا، خروجی فیلتر تطبیقی (y) با نویز موجود در سیگنال اصلی انطباق پیدا میکند و وقتی از سیگنال اصلی کم شود، سیگنال مطلوب را بدست میدهد.
[1] noise cancellation
[2] additive
- به منظور شناسایی سیستم[1]:همانطور که در شکل 4-2 به تصویر کشیده شده است، این ساختار برای شناسایی سیستم و مدل کردن آن به کار میرود. ورودیهای یکسان هم به سیستم مجهول و هم به فیلتر تطبیقی داده میشود و تفاضل خروجیها مجدداً به فیلتر بازخورد پیدا میکند تا ضرایب فیلتر را بهروز کند و در نهایت فیلتر تطبیقی مطابق با سیستم مجهول و ویژگیهایی همانند آن خواهیم داشت
[1] system identification
- پیشگوییکننده تطبیقی[1]: در این کاربرد، فیلتر تطبیقی به جهت پیدا کردن تقریبی از ورودی به سیستم بهکار میرود. بطوریکه سیستم در هر لحظه با توجه به ورودیهای قبلی، تقریبی از ورودی بعدی را به دست میدهد. بلوک دیاگرام کلی این فیلتر در شکل زیر آمده است:
[1] adaptive predictor
- فیلتر ناچ[1] با استفاده از دو ضریب: این ساختار برای حذف یا تضعیف نویز سینوسی به کار برده میشود و تنها شامل دو ضریب است که حجم محاسباتی بسیار کمتر از ساختار اول دارد. در شکل زیر ساختار این فیلتر آمده است:
[1] notch filter
الگوریتم LMS:
اگرچه فیلتر LMS معرفی شده برای بسیاری از کاربردهایی نظیر حذف نویز، حذف اکو[1] و پیشبینی سیگنال کاربرد دارد، اما انواع دیگری از این الگوریتم برای کاربردهای خاص مورد استفاده قرار میگیرند:
- الگوریتم sign-error که در آن به جای استفاده از سیگنال خطا در الگوریتم اصلی، از تابع علامت آن استفاده میشود:
- الگوریتم sign-data که در آن به جای استفاده از سیگنال ورودی در الگوریتم اصلی، از تابع علامت آن استفاده میشود:
- الگوریتم sign-sign که در آن از تابع علامت ورودی و خطا در الگوریتم اصلی استفاده میشود:
که در روش اخیر هنگامیکه ورودی و خطا هر دو هم علامت باشند، ضرایب جدید فیلتر به صورت زیر خواهند بود:
و اگر یکی از آنها علامت مخالف داشته باشد، ضرایب به صورت زیر بهروز میشوند:
سه الگوریتم اصلاح شدهای که در بالا به آنها اشاره شد، در کاربردی که مدنظر این پروژه است با توجه به شبیه سازیهای انجام شده و به دلیل نوع پردازنده استفاده شده و نوع سیگنال مورد پردازش مناسب نیستند. بنابراین در این پروژه از الگوریتم اصلی ارائه شده در بالا استفاده شده است.
[1] echo cancellation
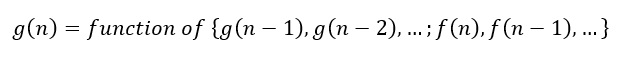

سلام
خسته نباشید
مطالبی که در مورد فیلتر قرار دادید بسیار جالب بود فقط اینکه چرا نمیتوان از روی آن کپی کرد؟؟
ودیگر اینکه آیا شما مطالبی در مورد شبکه های تطبیقی وترکیب فیلترهای تطبیقی هم دارید ممنون میشوم اگر امکان دارد برایم ارسال کنید؟؟(لطفا جواب را به ایمیلم ارسال نمایید.)
از لطف شما بی نهایت سپاسگزارم…
برای شما ایمیل شد
mamnon misham baray man ham email konid
agar az ketab ya manba dige estefade kardiid .lotfan esm manba ham zekr konid.mamnon
سلام ممنون از مطالب خوب شما اگر لطف کنید برام این مطلب را ایمیل کنید ممنون میشم
سلام…. میشه این مطالبرو بی زحمت برای منم ایمیل کنید… خیلی ازتون ممنون میشم
میتونید برای بنده هم ایمیل کنید ؟
سلام..میشه لطف کنید اگه کدهای متلب فیلتر وفقی lmsرو دلرین برام بفرستین…ممنون
سلام لطفا اگه میشه مطالب بیشتری در مورد الگوریتم وفقی LMSبرایم ارسال کنید . با تشکر از لطفتون.
سلام و خسته نباشید
مطالبتون عالی بود ،میخواستم کپی کنم اما نشد
میشود برایم ایمیل کنید
ممنونم
باعرض سلام.ببخشید من به این پستتون نیاز دارم میشه لطف کنین برام بفرستینش خدا خیرتون بده. شما مطلبی درمورد حذف نویز از سیگنال ecg دارید
سلام
به لینک زیر مراجعه فرمایید
لینک پایان نامه
سلام و خسته نباشید .. اگر چیزی پیدا کردید در این رابطه برای بنده هم بفرستید
سلام بسایر عالی ببخشید کدنویسی متلب راجع به الگوریتم lms دارین واسم بفرستین خیلی احتیاج دارم ممنون
سلام
ممنون از توضیحات .لطف میفرمایید برای بنده ایمیل نمایید
با تشکر
سلام
بسیار عالی
اگر امکانش هست برای منم ایمیل کنید
سلام مطالب جالب بوده و من هم با کپی و دانلود مطالب مشکل دارم، لطفا برای من هم ایمیل کنید. با تشکر
سلام، ببخشید ایا مطلبی راجع به الگوریتم و کد متلب numeric variable forgetting factor RLS; NVFFRLS دارین؟ احتیاج شدید دارم بهش، ممنون میشم برام ایمیل بفرمایید، سپاس فراوان
می شه این مطلب رو برای من ایمیل کنید
سلام میشه مطلب رو ایمیل کنید برای من؟
سلام خسته نباشید اگه براتون زحمتی نیست ممنون میشم مطلب بالا رو واسه منم ایمیل کنید
سلام . به شدت به این مطالب نیاز دارم. خواهشن برام ایمیل کنید . ممنون بابت توضیحات مفیدتون
سلام و خسته نباشید خدمت شما ..
برای بنده هم ارسال کنید..