شبکه های عصبی مصنوعی

شبکه عصبی مصنوعی روشی عملی برای یادگیری توابع گوناگون نظیر توابع با مقادیر حقیقی، توابع با مقادیر گسسته و توابع با مقادیر برداری میباشد.
یادگیری شبکه عصبی در برابر خطاهای داده های آموزشی مصون بوده و اینگونه شبکه ها با موفقیت به مسائلی نظیر شناسائی گفتار، شناسائی و تعبیر تصاویر، و یادگیری روبات اعمال شده است.

شبکه عصبی چیست؟
روشی برای محاسبه است که بر پایه اتصال به هم پیوسته چندین واحد پردازشی ساخته میشود.
شبکه از تعداد دلخواهی سلول یا گره یا واحد یا نرون تشکیل میشود که مجموعه ورودی را به خروجی ربط میدهند.

شبکه عصبی چه قابلیتهائی دارد ؟
محاسبه یک تابع معلوم
تقریب یک تابع ناشناخته
شناسائی الگو
پردازش سیگنال
یادگیری

مسائل مناسب برای یادگیری شبکه های عصبی
خطا در داده های آموزشی وجود داشته باشد. مثل مسائلی که داده های آموزشی دارای نویز حاصل از دادهای سنسورها نظیر دوربین و میکروفن ها هستند.
مواردی که نمونه ها توسط مقادیر زیادی زوج ویژگی-مقدار نشان داده شده باشند. نظیر داده های حاصل از یک دوربین ویدئوئی.
تابع هدف دارای مقادیر پیوسته باشد.
زمان کافی برای یادگیری وجود داشته باشد. این روش در مقایسه با روشهای دیگر نظیر درخت تصمیم نیاز به زمان بیشتری برای یادگیری دارد.
نیازی به تعبیر تابع هدف نباشد. زیرا به سختی میتوان اوزان یادگرفته شده توسط شبکه را تعبیر نمود.

الهام از طبیعت
مطالعه شبکه های عصبی مصنوعی تا حد زیادی ملهم از سیستم های یادگیر طبیعی است که در آنها یک مجموعه پیچیده از نرونهای به هم متصل در کار یادگیری دخیل هستند.
گمان میرود که مغز انسان از تعداد 10 11 نرون تشکیل شده باشد که هر نرون با تقریبا 104 نرون دیگر در ارتباط است.
سرعت سوئیچنگ نرونها در حدود 10-3 ثانیه است که در مقایسه با کامپیوترها 10 -10 ) ثانیه ( بسیار ناچیز مینماید. با این وجود آدمی قادر است در 0.1 ثانیه تصویر یک انسان را بازشناسائی نماید. این قدرت فوق العاده باید از پردازش موازی توزیع شده در تعدادی زیادی از نرونها حاصل شده باشد.

Perceptron
نوعی از شبکه عصبی برمبنای یک واحد محاسباتی به نام پرسپترون ساخته میشود. یک پرسپترون برداری از ورودیهای با مقادیر حقیقی را گرفته و یک ترکیب خطی از این ورودیها را محاسبه میکند. اگر حاصل از یک مقدار آستانه بیشتر بود خروجی پرسپترون برابر با 1 و در غیر اینصورت معادل -1 خواهد بود .

یادگیری پرسپترون عبارت است از:
پیدا کردن مقادیردرستی برای W
بنابراین فضای فرضیه H در یادگیری پرسپترون عبارت است ازمجموعه تمام مقادیر حقیقی ممکن برای بردارهای وزن.

توانائی پرسپترون
پریسپترون را میتوان بصورت یک سطح تصمیم hyperplane در فضای n بعدی نمونه ها در نظر گرفت. پرسپترون برای نمونه های یک طرف صفحه مقدار 1 و برای مقادیر طرف دیگر مقدار -1 بوجود میاورد.

توابعی که پرسپترون قادر به یادگیری آنها میباشد
یک پرسپترون فقط قادر است مثالهائی را یاد بگیرد که بصورت خطی جداپذیر باشند. اینگونه مثالها مواردی هستند که بطور کامل توسط یک hyperplaneقابل جدا سازی میباشند.

توابع بولی و پرسپترون
یک پرسپترون میتواند بسیاری از توابع بولی را نمایش دهد نظیر AND, OR, NAND, NOR
اما نمیتواند XORرا نمایش دهد.
در واقع هر تابع بولی را میتوان با شبکه ای دوسطحی از پرسپترونها نشان داد.

اضافه کردن بایاس
افزودن بایاس موجب میشود تا استفاده از شبکه پرسپترون با سهولت بیشتری انجام شود.
برای اینکه برای یادگیری بایاس نیازی به استفاده از قانون دیگری نداشته باشیم بایاس را بصورت یک ورودی با مقدار ثابت 1 در نظر گرفته و وزن W0 را به آن اختصاص میدهیم.

آموزش پرسپترون
چگونه وزنهای یک پرسپترون واحد را یاد بگیریم به نحوی که پرسپترون برای مثالهای آموزشی مقادیر صحیح را ایجاد نماید؟
دو راه مختلف :
قانون پرسپترون
قانون دلتا

آموزش پرسپترون
الگوریتم یادگیری پرسپترون
مقادیری تصادفی به وزنها نسبت میدهیم
پریسپترون را به تک تک مثالهای آموزشی اعمال میکنیم. اگر مثال غلط ارزیابی شود مقادیر وزنهای پرسپترون را تصحیح میکنیم.
آیا تمامی مثالهای آموزشی درست ارزیابی میشوند:
بله  پایان الگوریتم
خیربه مرحله 2 برمیگردیم

قانون پرسپترون
برای یک مثال آموزشیX = (x1, x2, …, xn) در هر مرحله وزنها بر اساس قانون پرسپترون بصورت زیر تغییر میکند:
wi = wi + Δwi

که در آن

Δwi = η ( t – o ) xi
t: target output
o: output generated by the perceptron
η: constant called the learning rate (e.g., 0.1)

 

اثبات شده است که برای یک مجموعه مثال جداپذیرخطی این روش همگرا شده و پرسپترون قادر به جدا سازی صحیح مثالها خواهد شد.

قانون دلتا Delta Rule
وقتی که مثالها بصورت خطی جداپذیر نباشند قانون پرسپترون همگرا نخواهد شد. برای غلبه بر این مشکل از قانون دلتا استفاده میشود.
ایده اصلی این قانون استفاده از gradient descent برای جستجو در فضای فرضیه وزنهای ممکن میباشد. این قانون پایه روش Backpropagation است که برای آموزش شبکه با چندین نرون به هم متصل بکار میرود.
همچنین این روش پایه ای برای انواع الگوریتمهای یادگیری است که باید فضای فرضیه ای شامل فرضیه های مختلف پیوسته را جستجو کنند.

برای درک بهتر این روش آنرا به یک پرسپترون فاقد حد آستانه اعمال میکنیم. در انجا لازم است ابتدا تعریفی برای خطا ی آموزش ارائه شود. یک تعریف متداول این چنین است:
E = ½ Σi (ti – oi) 2

که این مجموع برای تمام مثالهای آموزشی انجام میشود.

الگوریتم gradient descent
با توجه به نحوه تعریف E سطح خطا بصورت یک سهمی خواهد بود. ما بدنبال وزنهائی هستیم که حداقل خطا را داشته باشند . الگوریتم gradient descent در فضای وزنها بدنبال برداری میگردد که خطا را حداقل کند. این الگوریتم از یک مقدار دلبخواه برای بردار وزن شروع کرده و در هر مرحله وزنها را طوری تغییر میدهد که در جهت شیب کاهشی منحنی فوق خطا کاهش داده شود.

بدست آوردن قانون gradient descent
ایده اصلی: گرادیان همواره در جهت افزایش شیب E عمل میکند.
گرادیان E نسبت به بردار وزن w بصورت زیر تعریف میشود:

E (W) = [ E’/w0, E’/w1, …, E’/wn]
که در آن E (W) یک بردارو E’مشتق جزئی نسبت به هر وزن میباشد.

برای یک مثال آموزشیX = (x1, x2, …, xn) در هر مرحله وزنها بر اساس قانون دلتا بصورت زیر تغییر میکند:
wi = wi + Δwi

Where Δwi = -η E’(W)/wi

η: learning rate (e.g., 0.1)
علامت منفی نشان دهنده حرکت در جهت کاهش شیب است.

محاسبه گرادیان
با مشتق گیری جزئی از رابطه خطا میتوان بسادگی گرادیان را محاسبه نمود:
E’(W)/ wi = Σi (ti – Oi) (-xi)
لذا وزنها طبق رابطه زیر تغییر خواهند نمود.
Δwi = η Σi (ti – oi) xi

خلاصه یادگیری قانون دلتا
الگوریتم یادگیری با استفاده از قانون دلتا بصورت زیر میباشد.
به وزنها مقدار تصادفی نسبت دهید
تا رسیدن به شرایط توقف مراحل زیر را ادامه دهید
هر وزن wi را با مقدار صفر عدد دهی اولیه کنید.
برای هر مثال: وزن wi را بصورت زیر تغییر دهید:
wi = wi + η (t – o) xi
مقدار wi را بصورت زیر تغییر دهید:
wi = wi + wi
تا خطا بسیار کوچک شود

مشکلات روش gradient descent
ممکن است همگرا شدن به یک مقدار مینیمم زمان زیادی لازم داشته باشد.
اگر در سطح خطا چندین مینیمم محلی وجود داشته باشد تضمینی وجود ندارد که الگوریتم مینیمم مطلق را پیدا بکند.

در ضمن این روش وقتی قابل استفاده است که:
فضای فرضیه دارای فرضیه های پارامتریک پیوسته باشد.
رابطه خطا قابل مشتق گیری باشد

تقریب افزایشی gradient descent
میتوان بجای تغییر وزنها پس از مشاهده همه مثالها، آنها را بازا هر مثال مشاهده شده تغییر داد. در این حالت وزنها بصورت افزایشی incremental تغییر میکنند. این روش را stochastic gradient descent نیزمینامند.
wi = η (t-o) xi
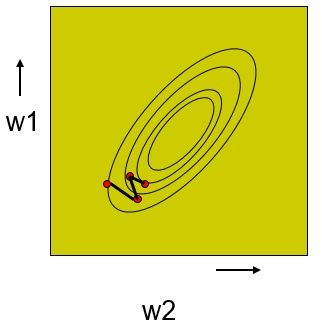
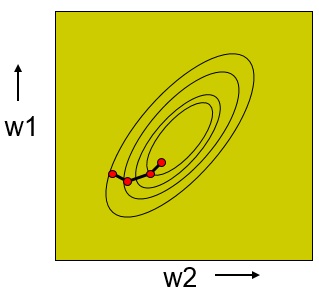
در بعضی موارد تغییر افزایشی وزنها میتواند از بروز مینیمم محلی جلوگیری کند. روش استاندارد نیاز به محاسبات بیشتری دارد درعوض میتواند طول step بزرگتری هم داشته باشد.

مقایسه آموزش یکجا و افزایشی
آموزش افزایشی (Online learning)

آموزش یکجا (Batch learning)

شبکه های چند لایه
بر خلاف پرسپترونها شبکه های چند لایه میتوانند برای یادگیری مسائل غیر خطی و همچنین مسائلی با تصمیم گیری های متعدد بکار روند.

یک سلول واحد
برای اینکه بتوانیم فضای تصمیم گیری را بصورت غیر خطی از هم جدا بکنیم، لازم است تا هر سلول واحد را بصورت یک تابع غیر خطی تعریف نمائیم. مثالی از چنین سلولی میتواند یک واحد سیگموئید باشد:

تابع سیگموئید
خروجی این سلول واحد را بصورت زیر میتوان بیان نمود:

تابع σ تابع سیگموئید یا لجستیک نامیده میشود. این تابع دارای خاصیت زیر است:

الگوریتم Back propagation
برای یادگیری وزن های یک شبکه چند لایه از روش Back Propagation استفاده میشود. در این روش با استفاده از gradient descent سعی میشود تا مربع خطای بین خروجی های شبکه و تابع هدف مینیمم شود.
خطا بصورت زیر تعریف میشود:

مراد ازoutputs خروجیهای مجموعه واحد های لایه خروجی و tkdو okd مقدار هدف و خروجی متناظر با k امین واحد خروجی و مثال آموزشی d است.

الگوریتم Back propagation
فضای فرضیه مورد جستجو در این روش عبارت است از فضای بزرگی که توسط همه مقادیر ممکن برای وزنها تعریف میشود. روش gradient descent سعی میکند تا با مینیمم کردن خطا به فرضیه مناسبی دست پیدا کند. اما تضمینی برای اینکه این الگوریتم به مینیمم مطلق برسد وجود ندارد.

الگوریتم BP
شبکه ای با ninگره ورودی، nhidden گره مخفی، و nout گره خروجی ایجاد کنید.
همه وزنها را با یک مقدار تصادفی کوچک عدد دهی کنید.
تا رسیدن به شرط پایانی ) کوچک شدن خطا( مراحل زیر را انجام دهید:
برای هر xمتعلق به مثالهای آموزشی:
مثال X را به سمت جلو در شبکه انتشار دهید
خطای E را به سمت عقب در شبکه انتشار دهید.

هر مثال آموزشی بصورت یک زوج (x,t) ارائه میشود که بردار x مقادیر ورودی و بردار t مقادیر هدف برای خروجی شبکه را تعیین میکنند.

انتشار به سمت جلو
برای هر مثال X مقدار خروجی هر واحد را محاسبه کنید تا به گره های خروجی برسید.

انتشار به سمت عقب
برای هر واحد خروجی جمله خطا را بصورت زیر محاسبه کنید: δk = Ok (1-Ok)(tk – Ok)
برای هر واحد مخفی جمله خطا را بصورت زیر محاسبه کنید: δh = Oh (1-Oh) Σk Wkh δk
مقدارهر وزن را بصورت زیر تغییر دهید:
Wji = Wji + ΔWji
که در آن :
ΔWji = η δj Xji

ηعبارت است از نرخ یادگیری

شرط خاتمه
معمولا الگوریتم BP پیش از خاتمه هزاران بار با استفاده همان داده های آموزشی تکرار میگردد شروط مختلفی را میتوان برای خاتمه الگوریتم بکار برد:
توقف بعد از تکرار به دفعات معین
توقف وقتی که خطا از یک مقدار تعیین شده کمتر شود.
توقف وقتی که خطا در مثالهای مجموعه تائید از قاعده خاصی پیروی نماید.
اگر دفعات تکرار کم باشد خطا خواهیم داشت و اگر زیاد باشد مسئله Overfitting رخ خواهد داد.

.

منحنی یادگیری

.

مرور الگوریتم BP
این الگوریتم یک جستجوی gradient descent در فضای وزنها انجام میدهد.
ممکن است در یک مینیمم محلی گیر بیافتد
در عمل بسیار موثر بوده است

.

برای پرهیز از مینیمم محلی روشهای مختلفی وجود دارد:
افزودن ممنتم
استفاده از stochastic gradient descent
استفاده ازشبکه های مختلف با مقادیر متفاوتی برای وزنهای اولیه

.

افزودن ممنتم
میتوان قانون تغییر وزنها را طوری در نظر گرفت که تغییر وزن در تکرار n ام تا حدی به اندازه تغییروزن در تکرار قبلی بستگی داشته باشد.
ΔWji (n) = η δj Xji + αΔWji (n-1)

که در آن مقدارممنتم α بصورت 0 <= α <= 1 میباشد.
افزودن ممنتم باعث میشود تا با حرکت در مسیر قبلی در سطح خطا:
از گیر افتادن در مینیم محلی پرهیز شود
از قرارگرفتن در سطوح صاف پرهیز شود
با افزایش تدریجی مقدار پله تغییرات، سرعت جستجو افزایش یابد.

.

قدرت نمایش توابع
گرچه قدرت نمایش توابع به توسط یک شبکه feedforward بسته به عمق و گستردگی شبکه دارد، با این وجود موارد زیر را میتوان به صورت قوانین کلی بیان نمود:
توابع بولی: هر تابع بولی را میتوان توسط یک شبکه دو لایه پیاده سازی نمود.
توابع پیوسته: هر تابع پیوسته محدود را میتوان توسط یک شبکه دو لایه تقریب زد. تئوری مربوطه در مورد شبکه هائی که از تابع سیگموئید در لایه پنهان و لایه خطی در شبکه خروجی استفاده میکنند صادق است.
توابع دلخواه: هر تابع دلخواه را میتوان با یک شبکه سه لایه تا حد قابل قبولی تفریب زد.
با این وجود باید درنظر داست که فضای فرضیه جستجو شده توسط روش gradient deescent ممکن است در برگیرنده تمام مقادیر ممکن وزنها نباشد.

.

فضای فرضیه و بایاس استقرا
فضای فرضیه مورد جستجو را میتوان بصورت یک فضای فرضیه اقلیدسی n بعدی از وزنهای شبکه در نظر گرفت )کهn تعداد وزنهاست(
این فضای فرضیه بر خلاف فضای فرضیه درخت تصمیم یک فضای پیوسته است.
بایاس استقرا این روش را میتوان بصورت زیر بیان کرد:
“smooth interpolation between data points”
به این معنا که الگوریتم BP سعی میکند تا نقاطی را که به هم نزدیکتر هستند در یک دسته بندی قرار دهد.

.

قدرت نمایش لایه پنهان
یکی از خواص BP این است که میتواند در لایه های پنهان شبکه ویژگیهای نا آشکاری از داده ورودی نشان دهد.
برای مثال شبکه 8x3x8 زیر طوری آموزش داده میشود که مقدارهرمثال ورودی را عینا در خروجی بوجو د آورد )تابع f(x)=x را یاد بگیرد(. ساختار خاص این شبکه باعث میشود تا واحد های لایه وسط ویژگی های مقادیر ورودی را به نحوی کد بندی کنند که لایه خروحی بتواند از آنان برای نمایش مجدد داده ها استفاده نماید.

.

قدرت تعمیم و overfitting
شرط پایان الگوریتم BP چیست؟
یک انتخاب این است که الگوریتم را آنقدر ادامه دهیم تا خطا از مقدار معینی کمتر شود. این امر میتواند منجر به overfitting شود.

 

 

 
دلایل رخ دادن overfitting
overfitting ناشی از تنظیم وزنها برای در نظر گرفتن مثالهای نادری است که ممکن است با توزیع کلی داده ها مطابقت نداشته باشند. تعداد زیاد وزنهای یک شبکه عصبی باعث میشود تا شبکه درجه آزادی زیادی برای انطباق با این مثالها داشته باشد.
با افزایش تعداد تکرار، پیچیدگی فضای فرضیه یادگرفته شده توسط الگوریتم بیشتر و بیشتر میشود تا شبکه بتواند نویز و مثالهای نادر موجود در مجموعه آموزش را بدرستی ارزیابی نماید.

 

راه حل
استفاده از یک مجموعه تائید Vallidation و توقف یادگیری هنگامی که خطا در این مجموعه به اندازه کافی کوچک میشود.
بایاس کردن شبکه برای فضاهای فرضیه ساده تر: یک راه میتواند استفاده از weight decayباشد که در آن مقدار وزنها در هر بارتکرار باندازه خیلی کمی کاهش داده میشود.
k-fold cross validation وقتی که تعداد مثالهای آموزشی کم باشد میتوان m داده آموزشی را به K دسته تقسیم بندی نموده و آزمایش را به تعداد k دفعه تکرار نمود. در هر دفعه یکی از دسته ها بعنوان مجموعه تست و بقیه بعنوان مجموعه آموزشی استفاده خواهند شد. تصمیم گیری بر اساس میانگین نتایج انجام میشود.

 

روشهای دیگر

راه های بسیار متنوعی برای ایجاد شبکه های جدید وجود دارد از جمله:
استفاده از تعاریف دیگری برای تابع خطا
استفاده از روشهای دیگری برای کاهش خطا در حین یادگیری
Hybrid Global Learning
Simulated Annealing
Genetic Algorithms
استفاده از توابع دیگری در واحدها
Radial Basis Functions
استفاده از ساختار های دیگری برای شبکه
Recurrent Network